#11 - Linear Regression แบบเขียนมือ

Linear regression เป็นความสัมพันธ์แบบเชิงเส้นระหว่างค่าที่เราต้องการทำนาย กับตัวแปรที่เรานำมาใช้ในการคำนวณ เทคนิคนี้เป็นเทคนิคที่ใช้มานานแล้ว กับเป็นเทคนิคที่เป็นโมเดลทางคณิตศาสตร์ที่เข้าใจง่าย ร่วมกับใช้งานได้หลากหลาย ตั้งแต่การศึกษา ไปจนถึงธุรกิจต่าง ๆ
อย่างไรก็ดี ก่อนที่เราจะใช้โมเดลทางคณิตศาสตร์นี้ เราจำเป็นต้องพิจารณา
- ตัวแปรที่ใช้จะเป็นตัวแปรแบบ Continuous ได้แก่เวลา ยอดขาย น้ำหนัก คะแนนสอบ
- ใช้ Scatter plot เพื่อหาความสัมพันธ์เชิงเส้นระหว่างตัวแปรที่เราต้องการหาคำตอบ และตัวแปร Feature ที่ใช้คำนวณในโมเดล
- ข้อมูลที่ใช้ไม่มีค่าที่เป็น Outlier อย่างเห็นได้ชัด
- เช็คว่าติดเรื่อง Homoscedasticity ที่ค่า Variance ของตัวแปรมีค่าไม่คงที่
- ค่า Residuals (errors)
ขั้นตอนการเทรนโมเดล
เมื่อพิจารณาแล้วไม่มีปัญหา เรามาพิจารณาขั้นตอนการเทรนโมเดลแบบคร่าว ๆ
- นำข้อมูลจาก Dataset มาหา Features หรือตัวแปรที่เราต้องการนำมาใช้ (X) และหาผลลัพธ์ (Outcome) ที่เราต้องการทำนาย
- ใช้โมเดล Linear Regression ตำนวณเพื่อให้โมเดลทำนายออกมา
- ค่าที่ได้จากการทำนายจะถูกนำมาเทียบกับค่า Ground Truth ของ Dataset (หรือค่า Y) ด้วยการคำนวณ Cost Function
- นำ Cost Function มาหา Partial Derivative โดยพิจารณาจากตัวแปรค่า weight ของแต่ละ Feature (W) และค่า bias (b) แล้วคำนวณร่วมกับ Learning Rate เพื่อนำมาปรับค่า weight และ bias ด้วย Gradient Descent
- วนไปข้อ 2.) เพื่อให้โมเดลฝึกไปเรื่อย ๆ จนกว่าค่า Cost Function จะอยู่กับค่าเท่า ๆ เดิม หรือวนครบรอบ Epoch ตามที่ต้องการ
สมการ
เมื่อทราบขั้นตอนแล้ว เรามาดูสมการที่เกี่ยวข้องกับโมเดล Linear Regression ในแต่ละขั้นตอนครั
ขั้นตอนแรกคือการคำนวณค่าโดยใช้สมการโมเดล Linear Regression ตามด้านล่างนี้ในขั้นตอนที่ 2 (ในสมการใช้ตัวแปร Features เพียงตัวแปรเดียวเพื่อยกตัวอย่าง)
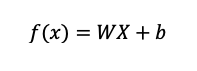
โดย
- W คือค่าพารามิเตอร์ weight ของแต่ละ Feature
- b คือค่าพารามิเตอร์ bias
- X คือค่าของตัวแปรที่เราต้องการนำมาใช้คำนวณในโมเดล
เมื่อทำนายค่าตามสมการด้านบนแล้ว เราต้องการนำค่าที่ได้เปรียบเทียบกับ Outcome (Y) ที่มีอยู่แล้วใน Dataset ด้วยการคำนวณสมการด้านล่างนี้ที่ใช้ Mean Square Error (MSE) เพื่อหา Cost Function ตามขั้นตอนที่ 3
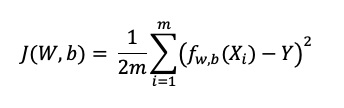
โดย
- fw,b เป็นฟังก์ชันที่ทำนายค่าตามขั้นตอนแรก
- Xi เป็นค่าตัวแปรที่เรานำมาใช้คำนวณ (X) ในแต่ละข้อมูลใน Dataset
- m คือจำนวนข้อมูลทั้งหมดใน Dataset
- Y คือค่า Ground Truth ที่เป็นผลลัพธ์ที่มีมาให้ใน Dataset
ถัดจากการได้ค่า Cost Function แล้ว เราจำเป็นต้องอัพเดทค่าพารามิเตอร์ในโมเดล Linear Regresion ด้วย Gradient Descent ตามขั้นตอนที่ 4 ที่สามารถเขียนรูปทั่วไปได้ตามข้างล่างนี้
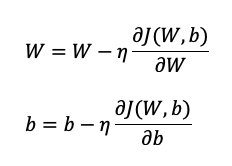
โดย
- W และ b คือพารามิเตอร์ weight และ bias
- J(w,b) คือ Cost Function
- ตัวคล้าย ๆ n คือ Learning rate
ในรูปทั่วไป เราจะเห็นตัว Partial Derivative ที่อยู่ทางด้านขวาของสมการ ที่นำสมการ Cost Function มาหา Derivative โดยเทียบกับตัวแปร W และตัวแปร b ที่สามารถเขียนวิธีการทำ Differentiate ได้ตามด้านล่างนี้
ส่วนแรกเป็น Partial Derivative ของ Cost Function โดยเทียบกับ W
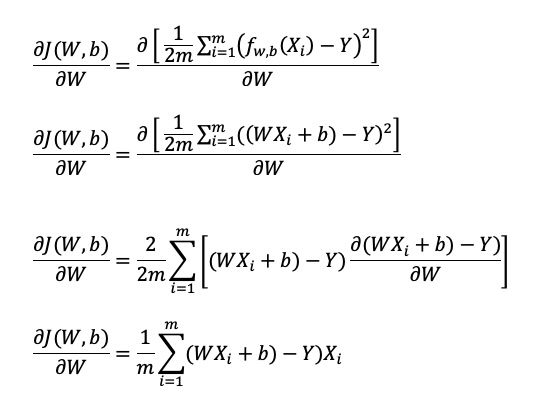
บรรทัดที่สาม เมื่อเราทำ Differentiate ของสมการที่ยกกำลังสองแล้ว เราจำเป็นต้อง Differentiate ตัวแปรข้างในวงเล็บอีกตามกฏ Chain Rule
ส่วนต่อมาเป็น Partial Derivative ของ Cost Function โดยเทียบกับ b
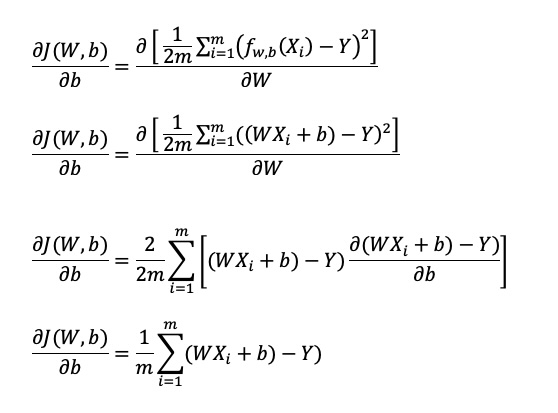
จากนั้น เรานำผลที่ได้จากการทำ Partial Derivative มาแทนที่ในสมการก่อนหน้า ผลลัพธ์ที่ได้เป็นตามด้านล่างนี้
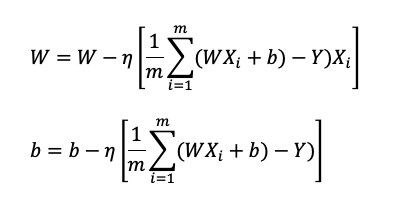
เมื่อได้สมการที่เกี่ยวข้องทั้งหมดแล้ว เรามาเขียนโค้ดใน Python โดยไม่ใช้คลาส LinearRegression ที่มีมาให้ใน Scikit-learn
การเขียนโค้ด
การเขียนโค้ดในที่นี่เราจะใช้ไลบรารี numpy เพื่อช่วยเรื่องการคำนวณให้เป็นแบบ Vectorization เพื่อเป็นการคำนวณทั้งอาเรย์ของ Weight (W), Features (X) เป็นต้น โดยไม่จำเป็นต้องวนลูปเข้าไปในอาเรย์ เราเขียนโค้ดการนำเข้าไลบรารีได้โดย
import numpy as np
from sklearn.model_selection import train_test_splitนำเข้าข้อมูลจาก Dataset
ในขั้นตอนแรก เราจะนำเข้าจาก Dataset อะไรก็ได้ โดยเปิดไฟล์จาก Excel (csv) เพื่อหา Features ที่ต้องการเพื่อนำไปมาใช้งานกับโมเดล Linear Regression ส่วนนี้ทำได้โดย
X, Y = [], []
with open("CSV path", "r") as f:
line_idx = 0
for line in f:
if line_idx == 0:
line_idx += 1
continue
line_idx += 1
line_split = line.strip().split(',')
X.append([float(x) for x in line_split[:-1]])
Y.append(float(line_split[-1]))
X, Y = np.array(X), np.array(Y)เมื่อโหลดข้อมูลมาอยู่ในตัวแปร X และ Y เรียบร้อยแล้ว เราจะนำค่าที่ได้มา Normalize โดยส่วนนี้จะไม่ได้กล่าวถึงในนี้ โดยตัวแปร
- X มีขนาดอาเรย์เท่ากับ [จำนวนข้อมูลที่มีใน Dataset (N_train), จำนวน Features (n_features)]
- Y มีขนาดอาเรย์เท่ากับ [จำนวนข้อมูลที่มีใน Dataset]
แบ่งข้อมูลใน Dataset
เมื่อทำเสร็จแล้วเราจะแบ่งข้อมูลที่มีใน Dataset โดยส่วนนี้เราแบ่งได้หลายวิธี เช่นแบ่งออกเป็น Train:Test ในอัตราส่วน 80:20, 70:30 หรือแบ่งออกเป็น Train:Validation:Test ในอัตราส่วน 70:20:10
ในตัวอย่างนี้เราจะแบ่งเป็น Train:Test ด้วยสัดส่วน 80:20 โดยใช้ฟังก์ชัน train_test_split จาก scikit-learn
การใช้งาน เราสามารถเขียนได้ตามด้านล่างนี้
X_train, X_test, Y_train, Y_test = train_test_split(
X, Y, test_size=0.2, random_state=1234
)โดย
- test_size = 0.2 คือการกำหนดว่าขนาดข้อมูล Test subset มีค่าเท่ากับ 20% ของข้อมูลทั้งหมด
- random_state = 1234 เป็นการกำหนด Random Seed โดยค่า Random Seed เป็นการกำหนดค่าเริ่มต้นของการสุ่ม เพื่อให้โปรแกรมสุ่มตัวเลขแบบเดิมเสมอ เนื่องมาจากไพทอนจะใช้การสุ่มแบบ Pseudorandom (โดยปกติจะใส่ค่า 0 หรือ 42 ซึ่งเลข 42 จริง ๆ มีที่มาจากหนังสือ The Hitchhiker’s Guide to the Galaxy ของ Douglas Adams ที่เขียนตอบคำถามที่เกี่ยวกับ Answer to the Ultimate Question of Life, the Universe, and Everything)
- X_train, Y_train คือตัวแปร X และ Y ของ Train subset ที่แบ่งออกมาจาก Dataset ในสัดส่วน 80% แรก
- X_test, Y_test คือตัวแปร X และ Y ของ Test subset ที่แบ่งออกมา 20% ของ Dataset ทั้งหมด
เขียนโค้ด Linear Regression
ต่อมา เรามาเขียนโค้ดส่วน Linear Regression ที่เกี่ยวข้องกับขั้นตอนที่ 2 – 5 ของการเทรนโมเดล Linear Regression
สร้างคลาส
ก่อนอื่น เรามาสร้างคลาสกันเสียก่อน โดยเขียนตามด้านล่างนี้
class LinearRegression:
def __init__(self, n_features = 8, learning_rate = 0.01, n_epochs = 100):
self.n_features = n_features
self.n_epochs = n_epochs
self.lr = learning_rate
self.weights = None
self.bias = None
def cost_function(self, y_hat, y):
pass
def predict(self, X):
pass
def fit(self, X_t, Y_t):
passโดย
- n_features คือการกำหนดจำนวน Features ที่ต้องการใช้เพื่อทำนายในโมเดล Linear Regression
- n_epochs คือจำนวนรอบที่ต้องการเทรนโมเดล
- learning_rate คือการกำหนดพารามิเตอร์ที่จำเป็นต้องการปรับค่า weight และ bias ของโมเดล
- weights และ bias คือค่า weight (W) และ bias (b) ของโมเดล
Cost Function
ต่อมา เรามาเขียนโค้ดส่วนฟังก์ชัน cost_function เพื่อคำนวณ Cost Function ของโมเดล Linear Regression ที่เราใช้ Mean Square Error (MSE)
def cost_function(self, y_hat, y):
return (np.square(y_hat - y)).mean() / 2โดย
- y_hat คือค่าที่โมเดลทำนายได้
- y คือค่า Ground Truth ที่เป็นผลลัพธ์ที่มีมาให้ใน Dataset
Training
เราสามารถเขียนโค้ดในฟังก์ชัน fit ที่ใช้สำหรับเทรนตัวโมเดลได้ตามด้านล่างนี้
def fit(self, X, Y):
cache = []
N_train, n_features = X.shape
self.W = np.random.rand(n_features)
self.b = 0
for i in range(self.n_epochs):
X_train = X.copy()
Y_train = Y.copy()
# Forward Propagation
y_hat = np.dot(X_train, self.W) + self.b
# Calculation of Cost Function
L = self.cost_function(y_hat, Y_train)
cache.append(L)
# Backpropagation y_hat/y_train -> [n_batch] X_train -> [n_batch, n_features]
dz = y_hat - Y_train
dw = (1 / N_train) * np.dot(X_train.T, dz)
db = (1 / N_train) * np.sum(dz)
# Update Parameters
self.W = self.W - self.lr * dw
self.b = self.b - self.lr * db
print(f"[*] Epoch {i+1}/{self.n_epochs} : Loss\t{L:.4f}") #\tAccuracy\t{accuracy:.4f}%")
return cacheโดย ส่วนแรกเป็นการกำหนดค่าพารามิเตอร์ weight (W) และ bias (b) ของตัวโมเดล
self.W = np.random.rand(n_features)
self.b = 0ส่วนต่อมาเป็นการให้ตัวโมเดลทำนายค่าตามที่เราใช้ใส่ข้อมูล Features (X) เข้าไป โดยเก็บตัวแปร X และ Y ไว้ในตัวแปร X_train และ Y_train
X_train = X.copy()
Y_train = Y.copy()
# Forward Propagation
y_hat = np.dot(X_train, self.W) + self.bเมื่อได้ผลจากการคำนวณในโมเดลแล้ว เรามาคำนวณ Cost Function โดย y_hat คือค่า
# Calculation of Cost Function
L = self.cost_function(y_hat, Y_train)หลังจากคำนวณใน Cost Function แล้ว เราอัพเดทพารามิเตอร์ weight (W) และ bias (b)
# Backpropagation y_hat/y_train -> [n_batch] X_train -> [n_batch, n_features]
dz = y_hat - Y_train
dw = (1 / N_train) * np.dot(X_train.T, dz)
db = (1 / N_train) * np.sum(dz)
# Update Parameters
self.W = self.W - self.lr * dw
self.b = self.b - self.lr * dbเมื่ออัพเดทพารามิเตอร์แล้ว เราก็จะให้วนลูปจนกว่าจะครบรอบตามที่กำหนดจากตัวแปร n_epochs
Predict
เมื่อเราเทรนโมเดลเสร็จเรียบร้อย เราก็ต้องนำโมเดลมาใช้ทำนายค่าใช่ไหมครับ?
ใช่ครับ เราสามารถเขียนโค้ดทำนายได้ไม่ยากเลย ด้วยการเขียนโค้ดตามด้านล่างนี้
def predict(self, X):
return np.dot(X, self.W) + self.bโดย X คือตัวแปรอาเรย์ Features ที่มีใน Dataset ส่วน W และ b คือค่า Weight และ bias
เมื่อเขียนโค้ดเสร็จแล้ว โค้ดจะมีหน้าตามด้านล่างนี้
class LinearRegression:
def __init__(self, n_features = 8, learning_rate = 0.01, n_epochs = 100):
self.n_features = n_features
self.n_epochs = n_epochs
self.lr = learning_rate
self.weights = None
self.bias = None
def cost_function(self, y_hat, y):
return (np.square(y_hat - y)).mean() / 2
def predict(self, X):
return np.dot(X, self.W) + self.b
def fit(self, X, Y):
cache = []
N_train, n_features = X.shape
self.W = np.random.rand(n_features)
self.b = 0
for i in range(self.n_epochs):
X_train = X.copy()
Y_train = Y.copy()
# Forward Propagation
y_hat = np.dot(X_train, self.W) + self.b
# Calculation of Cost Function
L = self.cost_function(y_hat, Y_train)
cache.append(L)
# Backpropagation y_hat/y_train -> [n_batch] X_train -> [n_batch, n_features]
dz = y_hat - Y_train
dw = (1 / N_train) * np.dot(X_train.T, dz)
db = (1 / N_train) * np.sum(dz)
# Update Parameters
self.W = self.W - self.lr * dw
self.b = self.b - self.lr * db
print(f"[*] Epoch {i+1}/{self.n_epochs} : Loss\t{L:.4f}")
return cacheผลลัพธ์
เมื่อเขียนโค้ดเสร็จแล้ว เราสามารถฝึกโมเดล และทดสอบโมเดลด้วยการเขียนโค้ดตามด้านล่างนี้ โดยเรากำหนดให้เทรนทั้งหมด 500 รอบ ด้วย Learning Rate เท่ากับ 0.005
learing_rate = 0.005
num_epoch = 500
model = LinearRegression(X_train.shape[-1], learning_rate, num_epoch)
cost = model.fit(X_train, Y_train)และเขียนโค้ดสำหรับการทดสอบตามด้านล่างนี้ โดยในตัวอย่างจะใช้การประเมินผลการทำนายจากโมเดล Linear Regression ด้วย Mean Absolute Error
from sklearn.metrics import mean_absolute_error
out = model.predict(X_test)
mae = mean_absolute_error(np.asarray(out), np.asarray(Y_test))
print(mae)ผลที่ได้จากการเทรน และการทดสอบก็แสดงตามด้านล่างนี้ โดยเราใช้ Dataset การทำนายน้ำหนักของสมอง ตามในเว็บ TowardsDataScience
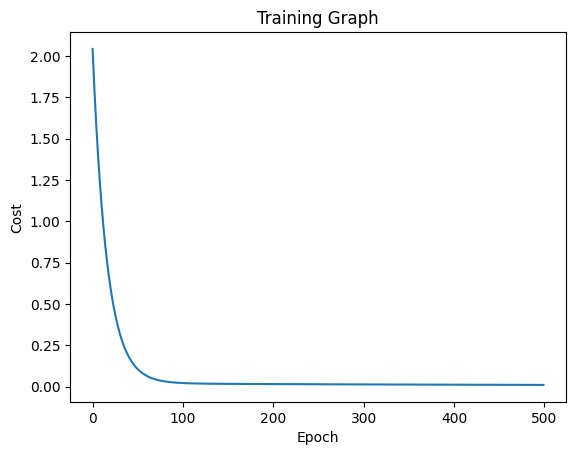
จากผลการฝึกพบว่าโมเดลเทรนโอเค พบว่าค่า Learning Rate สูงไปหน่อย อันนี้เราสามารถปรับ ๆ กันได้ทีหลัง
ส่วนต่อมาเป็นผลการทดสอบ พบว่าโมเดลสามารถทำนายด้วยค่า MAE เท่ากับ 220.164 ก็ถือว่าคลาดเคลื่อนไปหน่อย ซึ่งส่วนนี้เราสามารถปรับแต่งโมเดล ปรับพารามิเตอร์ ปรับแต่งการโหลด Dataset กันได้ทีหลังเช่นกัน
เสริม ลองใช้ Linear Regression จาก scikit-learn
ผู้อ่านสามารถเขียนโค้ดได้ง่ายเพียงไม่กี่บรรทัด โดยการเขียนโค้ดตามด้านล่างนี้
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model = model.fit(X_train, Y_train)
output = model.predict(X_test)
mae= mean_absolute_error(np.asarray(Y_test), np.asarray(output))
print(f"MAE {mae:.2f}")ผลลัพธ์ที่ได้ก็มีค่า MAE เท่ากับ 59.81 ถือว่าทำได้โอเค ส่วนถ้าต้องการอ่านข้อมูลเพิ่มเติม ผู้อ่านสามารถอ่านได้ในเว็บของ scikit-learn ได้ครับ
เสริม ลองใช้ Linear Regression สำหรับ Apple MLX
ผู้อ่านสามารถเข้าไปอ่านได้ที่ลิ้งค์นี้ครับ
© 2025. Nick Untitled. / Privacy Policy