#19 Big-O, Search & Sort ที่ใช้ในงาน Data

The English version of this blog related to the first part: Big-O notation, is available here.
เมื่อวันก่อนเข้าไปอ่านในหน้าเว็บ Medium ที่กล่าวถึง Data Structures & Algorithms (ย่อเป็น DSA) ที่จำเป็นสำหรับทาง Data Engineer ว่าต้องรู้เทคนิคไหนบ้าง แถมตอนเรียนในคอร์สจากเว็บ DataTH (รวมถึงที่อื่น) ก็มีกล่าวถึงไว้นิดหน่อยว่าจำเป็นต้องรู้เรื่องนี้ต่อยอดจากที่เรียนในคอร์ส
เราเลยสังเกตตอนที่เขียนโค้ดแล้วพบว่าโค้ดมันก็รันได้ แต่ประสิทธิภาพมันก็ไม่ได้ดีอะไรขนาดนั้น การมีความรู้ทางด้าน DSA ก็นำไปใช้ช่วยเขียนโค้ดให้ทำงานได้มีประสิทธิภาพมากกว่าเดิม โดยในบทความนี้ก็สรุป และแชร์เรื่องนี้ครับ
ก่อนอื่น เรามารู้กันก่อนว่าทำไมต้องรู้เรื่องนี้
สารบัญ
- เหตุผล
- Asymptotic Analysis
- Big-O Notation
- Searching Algorithm
- Sorting Algorithm
- สรุป
- แหล่งข้อมูลอ้างอิง
เหตุผล
เวลาที่เราเจอโจทย์ปัญหาอะไรก็ตาม สิ่งที่เราจะทำคือหาวิธีการแก้ไขปัญหา โดยจำเป็นต้องเลือกวิธีการแก้ปัญหาเป็นขั้นตอน 1 2 3 4 เพื่อให้เราแก้ไขปัญหาได้อย่างมีประสิทธิภาพมากที่สุด โดยโจทย์บางข้อเราสามารถใช้วิธีการแก้ไขปัญหาได้มากกว่า 1 วิธี
สิ่งนี้ เราเรียกการแก้ไขปัญหาตามข้างบนนั้นว่า Algorithms (หรือขั้นตอนวิธี) [1]
ต่อมา นอกจากเราเลือก Algorithm ที่เหมาะสมแล้ว เราจำเป็นต้องเลือกวิธีการเก็บ จัดการและเรียกใช้ข้อมูลคอมพิวเตอร์ที่เราเก็บไว้ เพื่อให้ตัว โค้ดใช้งานข้อมูลเหล่านั้นได้อย่างมีประสิทธิภาพมากที่สุด สิ่งนี้เราเรียกว่า Data Structures [1 – 3]
คำสองคำนี้ ได้แก่ Data Structures กับ Algorithms เป็นสิ่งที่ออกแบบมามีเป้าหมายหลักอันเดียวกันคือ แก้ปัญหาที่เราเจออยู่ ว่าแต่มันจะไปเกี่ยวกับงานทางด้าน Data Engineer (หรืองาน Data อื่น ๆ) อย่างไร?
ความรู้ด้านนี้มันจะเอาไปใช้กับงาน Data [4] ได้โดย
- เขียนโค้ดเพื่อจัดการ และประมวลผล Data ที่มีขนาดใหญ่ และซับซ้อนได้อย่างมีประสิทธิภาพ
- ปรับแต่ง Data Pipeline ให้ทำงานได้เร็วขึ้น และมีประสิทธิภาพขึ้นมากกว่าเดิม
- นำไปฝึกวิธีการแก้ไขปัญหา
- รวมถึงนำไปใช้งานกับงานทางด้านการประมวลผลแบบ Distributed Computing
หลังจากที่ทราบเหตุผลแล้ว เราแชร์เรื่องต่อไปที่จำเป็นคือ Asymptotic Analysis
Asymptotic Analysis
ประสิทธิภาพของการทำงานของ Algorithm ที่เราพัฒนาขึ้นมาแล้วนั้น เราสามารถวิเคราะห์ และอธิบายได้โดยการใช้ Asymptotic Notations [5, 6] ที่แต่ละ Algorithm ที่เรานำมาใช้เพื่อแก้ไขปัญหานั้นให้ประสิทธิภาพที่ไม่เท่านั้น โดยขึ้นอยู่กับลักษณะของข้อมูลที่เรานำมาใช้
Asymptotic Notations แบ่งออกได้เป็น 3 แบบ ตามการวัดประสิทธิภาพ ได้แก่ Big-O Notation (O) กับ Omega-Notation (Ω) และ Theta-Notation (Θ)
Big-O Notation (O) เป็นการระบุทรัพยากรที่ใช้ของ Algorithm นั้น ๆ เพื่อเทียบความสัมพันธ์ระหว่างระยะเวลา กับขนาดของ Input โดยคิดในกรณีที่ใช้ระยะเวลาในการทำงานมากที่สุด (Upper Bound) หรือใช้วัดในกรณีที่ประสิทธิภาพแย่ที่สุด (Worst Case)
ตัวอย่างเช่น Algorithm A มีประสิทธิภาพการทำงานเป็น O(N^2) ถ้าเรามีข้อมูลทั้งหมด 10 ข้อมูล แล้ว Algorithm นั้นจะใช้ระยะเวลาการทำงานที่ช้าที่สุดเป็น 100 หน่วยเวลา
Omega Notation (Ω) ที่ใช้สำหรับการระบุระยะเวลาที่ใช้กับ Algorithm นั้นน้อยที่สุด (Lower Bound) เมื่อทำงานกับ Input ขนาดหนึ่ง โดยวัดเมื่อ Algorithm นั้น ๆ ทำงานได้ดีที่สุด (Best Case)
ตัวอย่างเช่น Algorithm A มีประสิทธิภาพการทำงาน Ω(N) กรณีที่มีข้อมูลทั้งหมด 10 ข้อมูล ตัว Algorithm นี้จะใช้ระยะเวลาที่เร็วสุด 10 หน่วยเวลา โดยเราสามารถเขียนได้ว่า f(N) є Ω(A(N)) เพื่อบ่งบอกว่าฟังก์ชันของ N เป็นฟังก์ชันที่ไม่โต กับไม่ช้ากว่าฟังก์ชัน A(N)
Theta Notation (Θ) สำหรับการวัดประสิทธิภาพที่อยู่ระหว่าง Best Case กับ Worst Case (Average Case หรือเรียกอีกอย่างว่า Average Time Complexity)
การใช้ Theta Notation นี้ เราใช้ได้ในกรณีที่ Upper Bound และ Lower Bound อธิบาย Algorithm เดียวกัน กล่าวคือเราสามารถแสดงความสัมพันธ์ของเวลาการทำงานได้ว่า
“f(N) = Θ(A(N)) ก็ต่อเมื่อ f(N) = O(A(N)) และ f(N) = Ω(A(N))”
Big-O Notation
ในบทความนี้ เราจะใช้ Big-O Notation [6] สำหรับการอธิบาย Algorithm แต่ละ Algorithm เป็นหลัก โดยเราสามารถอธิบายลักษณะการทำงานของ Algorithm แต่ละ Algorithm ตามระยะเวลาที่ใช้ได้เป็น
- Constant (O(c)) สำหรับ Algorithm ที่ใช้ระยะเวลาเป็นค่าคงที่
- Logarithmic (O(log N)) สำหรับเทคนิคที่ใช้เวลาเป็นฟังก์ชันลอการิทึม
- Linear (O(N)) สำหรับเทคนิคที่ใช้เวลาเป็นฟังก์ชันเชิงเส้น
- Polynomial สำหรับเทคนิคที่ใช้ระยะเวลาเป็นฟังก์ชันยกกำลัง 2 (Quadratic, O(N^2)), 3 (Cubic, O(N^3)) หรืออื่น ๆ
- Exponential (O(2^N))
- Factorial (O(N!))
โดยเมื่อเรียงลำดับตามระยะเวลาที่ใช้แล้ว เราเรียงลำดับได้ตามด้านล่างนี้
Constant < Logarithmic < Linear < Quadratic < Cubic < Exponential < Factorial
เราสามารถสรุปได้เป็นกราฟตามด้านล่างนี้
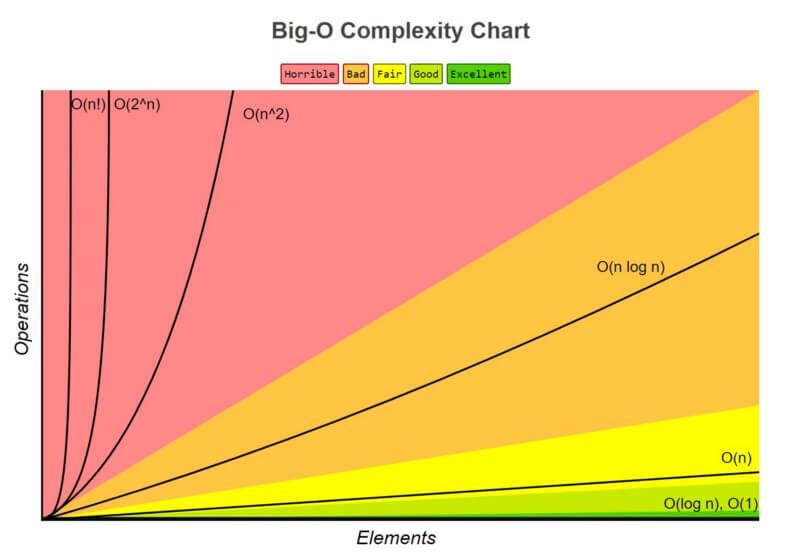
อย่างไรก็ดี กรณีที่ Big-O เป็น Exponential แบบ O(N^N) อันนี้จะใช้ระยะเวลาเพิ่มขึ้นเร็วมากกว่าฟังก์ชัน Factorial ในกรณีที่มีข้อมูล Input เพิ่มขึ้น
คุณสมบัติของ Big-O Notation [7] ได้แก่
- Constant Multiplication: เมื่อ f(n) = c * g(n) แล้ว O(f(n)) = O(g(n)) (ในกรณีที่ c ไม่เท่ากับ 0).
- Polynomial Function: เมื่อ f(n) = a₀ + a₁n + a₂n² + … + aₘnᵐ แล้ว O(f(n)) = O(nᵐ).
- Summation Function: เมื่อ f(n) = f₁(n) + f₂(n) + … + fₘ(n) และ fᵢ(n) ≤ fᵢ₊₁(n) สำหรับทุก ๆ ค่าของ i แล้ว O(f(n)) = O(max(f₁(n), f₂(n), …, fₘ(n))).
- Logarithmic Function: เมื่อ f(n) = logₐ(n) และ g(n) = log_b(n) แล้ว O(f(n)) = O(g(n)) (เมื่อฟังก์ชันทุกฟังก์ชันเพิ่มขึ้นพอ ๆ กัน).
การคำนวณหา Big-O Notation [8] เราทำได้โดย
- กรณีที่มีลูปซ้อนลูป (Nested Loop) ให้นำมาคูณกัน
- กรณีที่อยู่ลูประดับเดียวกันให้นำมาบวกกัน
- เมื่อรวมเสร็จแล้ว เราจะพบว่ามี Big-O Notation หลายอัน ให้ดูตัวที่แย่ที่สุด (Worst Case) เช่น O(n^2) + O(n) + O(n log n) เราจะได้เป็น O(n^2) ตาม Summation Function
- ไม่ต้องสนใจค่าที่เป็น Constant ได้แก่ If, switch หรือ Operator อื่นใด
- การเรียกใช้ฟังก์ชันนั้น ๆ ให้คำนวณ Big O ข้างในฟังก์ชันเพิ่มอีกด้วย
การนำไปใช้งาน Big-O Notation นั้น นอกจากเราเอาไปวิเคราะห์ระยะเวลาที่ใช้ของ Algorithm นั้น ๆ ได้แล้ว เรายังเอามาวิเคราะห์ดูการใช้พื้นที่หน่วยความจำของแต่ละ Algorithm อีกด้วย (Space Complexity) [9] ตัวอย่างเช่นเทคนิค Bucket Sort (ที่เราไม่ได้กล่าวถึงในบทความนี้) ใช้ Space Complexity เท่ากับ O(n) แต่เราสามารถปรับการทำงานให้เหลือ O(1) ได้
ต่อมา เรามาแชร์เรื่อง Algorithm Searching กับ Sorting ครับ ส่วน Data Structure กับ Algorithm อื่น เราไม่ได้กล่าวถึงในนี้
Searching Algorithm
Searching Algorithm เป็น Algorithm ที่ใช้ในการข้อมูลใน Array ตามที่เราต้องการ
Array คือ Data Structure รูปแบบหนึ่งที่เก็บข้อมูลที่ชนิดตัวแปรเหมือน ๆ กันอยู่ในตำแหน่งของหน่วยความจำที่อยู่ติดกัน (Contiguous Memory Locations)
Introduction to Arrays – Data Structure and Algorithm Tutorials – GeeksforGeeks
ตัวอย่างของ Searching Algorithm ในบทความนี้ ได้แก่ Linear Search, Binary Search และ Fibonacci Search โดยเทคนิค Search 2 อันหลังใช้ในกรณีที่ข้อมูลได้รับการเรียงลำดับ (Sorted) แล้ว
Linear Search
Linear Search [10] เป็นเทคนิคการหาข้อมูลใน Array โดยเรียงตามลำดับตั้งแต่ Array index ที่ 0, 1, 2, 3, … ไปจนถึง Array ตามที่เราต้องการหาข้อมูล

เราเขียนโค้ดได้ตามด้านล่างนี้
def linear_search(arr, find):
for idx, arr_each in enumerate(arr):
if arr_each == find:
return idx
return -1โดย -1 ใช้ในกรณีที่หาข้อมูลนั้น ๆ ไม่เจอ
Algorithm นี้มีประสิทธิภาพการทำงานตามระยะเวลาการทำงาน (Time Complexity) เท่ากับ O(n) และมี Space Complexity เท่ากับ O(1)
Binary Search
Binary Search [11] เป็นเทคนิคการหาข้อมูลใน Array ที่ผ่านการเรียงข้อมูลมาเรียบร้อยแล้ว (Sorted) โดยการแบ่งข้อมูลการค้นหาทีละครึ่งจนกว่าจะถึงข้อมูลที่ต้องการ ทำให้เทคนิคนี้มีประสิทธิภาพดีมากกว่าเทคนิค Linear Search ก่อนหน้า
ขั้นตอนการทำงาน*
เราสามารถสรุปการทำงานได้ตามตัวอย่างด้านล่างนี้
จากโจทย์ เราต้องการหาข้อมูลที่เป็นเลข 4
ขั้นตอนแรก เราหาข้อมูลที่อยู่ตรงกลางของ Array โดยการหารแล้วปัดเศษลง (Floor Division)
เราสามารถทำแบบนี้ใน Python ได้โดยการใช้เครื่องหมาย // โดยผลลัพธ์จะได้เป็นตัวแปรประเภท Integer (หรือจำนวนเต็ม)
ผลลัพธ์ที่ได้จากการหารนี้จะได้ค่าเท่ากับ 4 ตำแหน่งนี้ได้ Array จะมีค่าเท่ากับ 5 โดย 5 มีค่ามากกว่า 4 ดังนั้นแล้วเราจะแบ่งข้อมูลไปทางซ้าย (ไม่รวม 5)
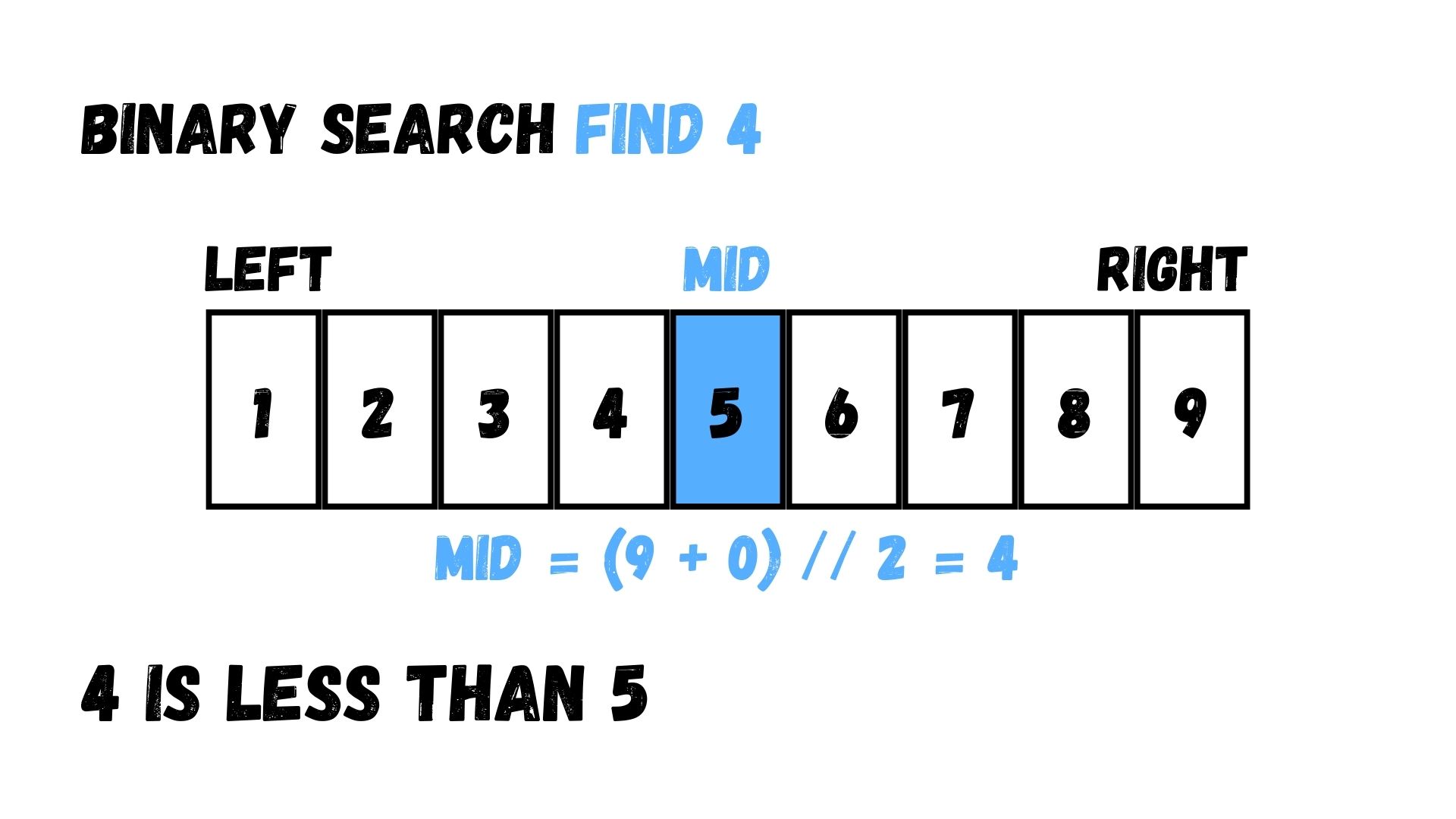
ต่อมา เราเลือกค่าที่อยู่ตรงกลางของ Array อีกเช่นเคย ผลลัพธ์ที่ได้จากการหารแบบนี้จะมีค่าเท่ากับ 1 ค่าที่ได้ในตำแหน่งที่ 1 ของ Array จะมีค่าเท่ากับ 2 ซึ่งน้อยกว่าค่าที่เราต้องการหา ให้เราแบ่งข้อมูลไปทางขวา

ต่อมา เราทำแบบเดียวกันกับในขั้นตอนที่ 1 ผลลัพธ์ที่ได้จะมีค่าเท่ากับ 2 ตำแหน่งที่ 2 ใน Array นี้จะมีค่าเท่ากับ 3 ซึ่งน้อยกว่าค่าที่เราต้องการหา ให้เราแบ่งครึ่งไปทางขวาอีกรอบหนึ่ง
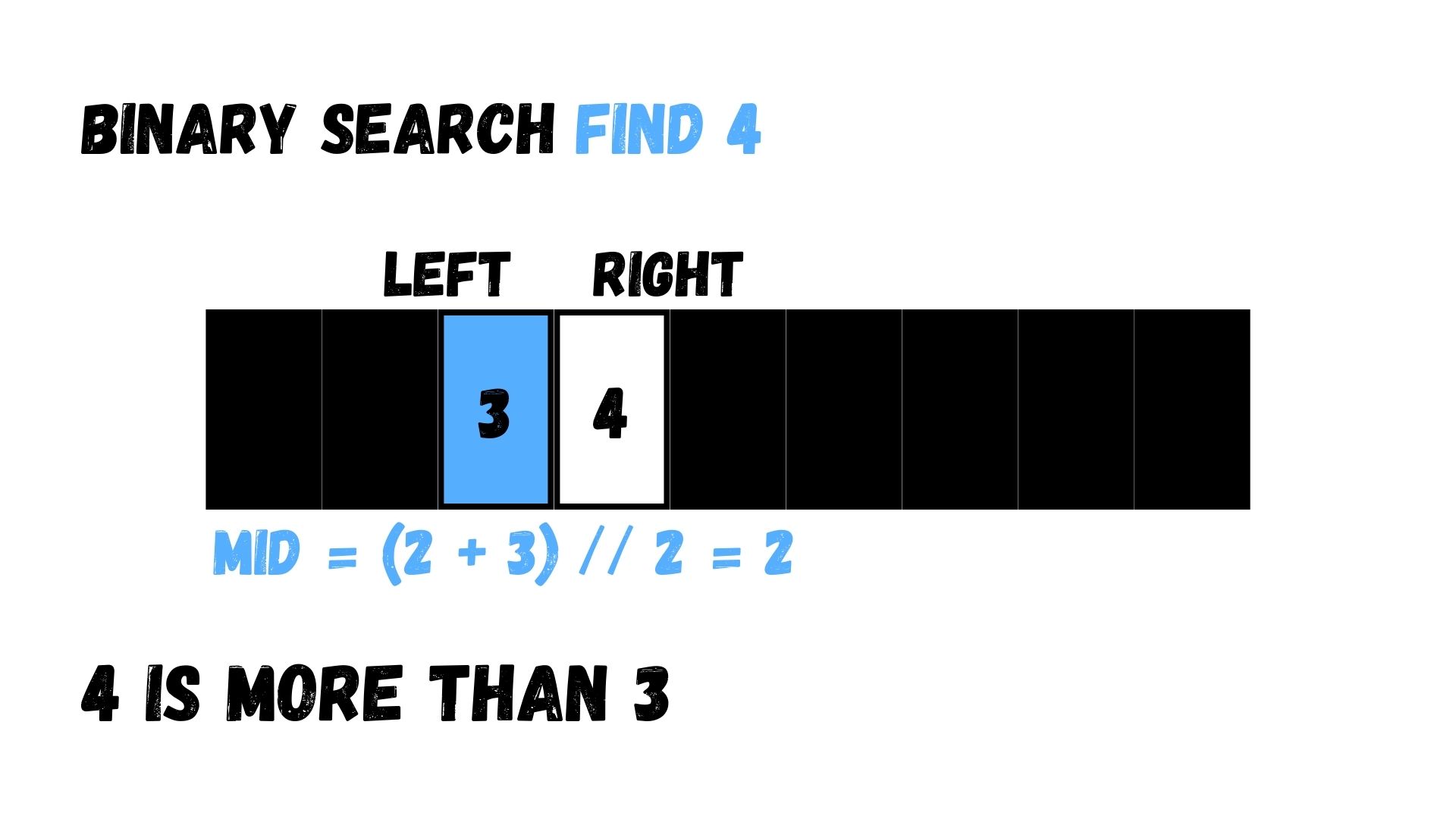
ต่อมา เราทำแบบเดียวกันกับในขั้นตอนที่ 1 ผลลัพธ์ที่ได้มีค่าเท่ากับ 3 ค่าที่ได้ในตำแหน่งนี้ของ Array มีค่าเท่ากับ 4 ก็เท่ากับเลขที่เราต้องการหาใน Array
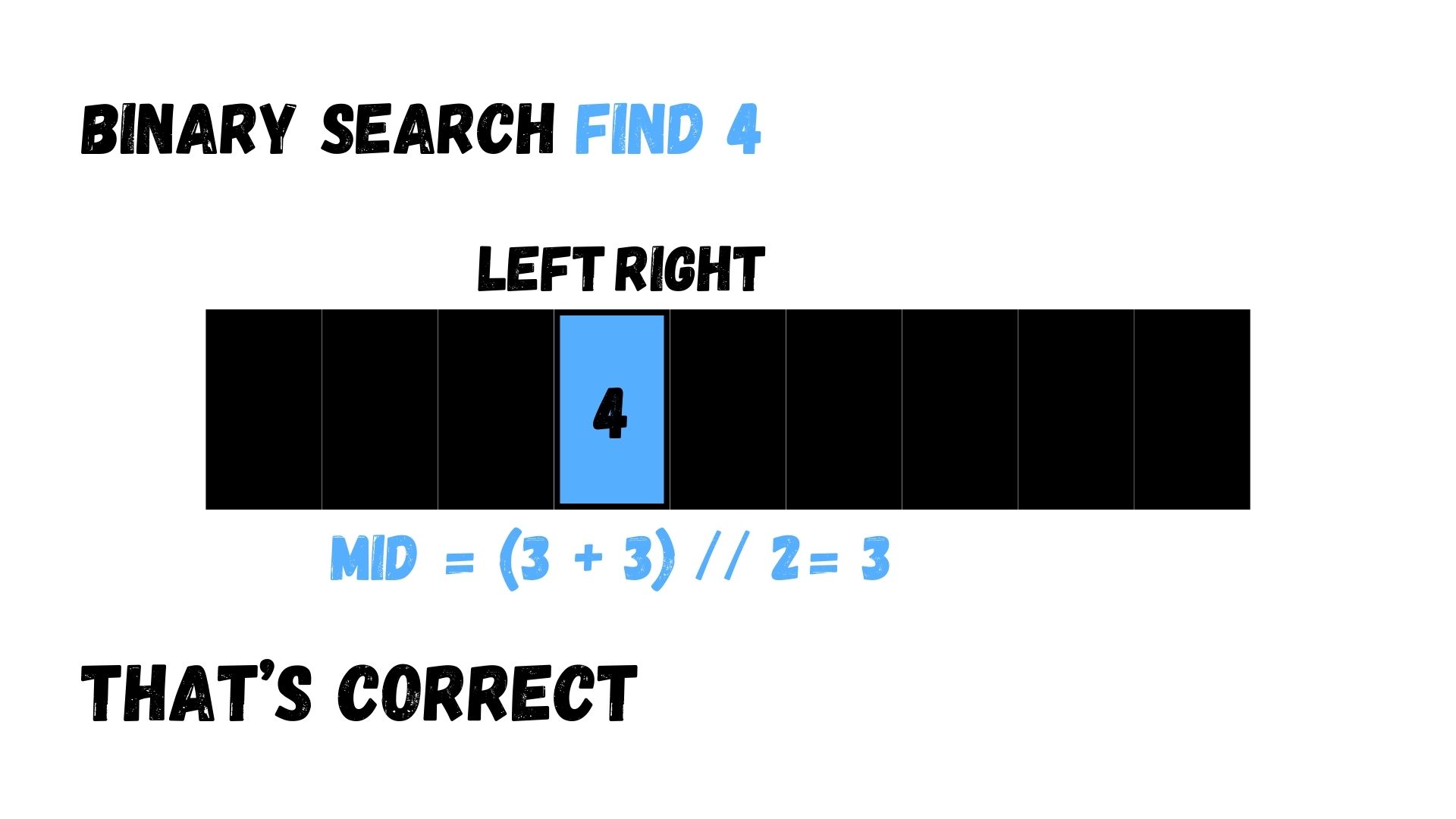
การเขียนโค้ด เราเขียนโค้ดได้ตามด้านล่างนี้
def binary_search(sorted_arr, find):
low = 0
high = len(sorted_arr)
while high - low > 0:
mid_arr = (low + high) // 2
if find == sorted_arr[mid_arr]:
return mid_arr
if find > sorted_arr[mid_arr]:
low = mid_arr + 1
if find < sorted_arr[mid_arr]:
high = mid_arr - 1
mid_arr = (low + high) // 2
if find == sorted_arr[mid_arr]:
return mid_arr
return -1Algorithm นี้มีประสิทธิภาพการทำงานตามระยะเวลาการทำงาน (Time Complexity) ในกรณีที่เป็น
- Best Case เท่ากับ O(1)
- Average และ Worst Case เท่ากับ O(log n)
และมี Space Complexity เท่ากับ O(1) ยกเว้นในกรณีที่รันผ่านการใช้ Recursion ที่จะใช้ Space Complexity เท่ากับ O(log n) [12]
ข้อดีของ Binary Search คือเป็นเทคนิคการค้นหาข้อมูลที่มีประสิทธิภาพโดยค้นหาข้อมูลได้เร็วมากกว่าแบบ Linear Search ทำให้ Algorithm นี้เหมาะสมสำหรับข้อมูลที่มีขนาดใหญ่
อย่างไรก็ดี เทคนิคนี้มีข้อเสีย ได้แก่
- ข้อมูลที่เรานำมาใช้ต้องเรียงข้อมูลให้เรียบร้อยเสียก่อน
- ข้อมูลที่นำมาใช้งานนั้นจำเป็นต้องเก็บไว้ในหน่วยความจำ
- ข้อมูลที่นำมาเปรียบเทียบนั้นจำเป็นต้องเปรียบเทียบข้อมูลมากน้อยได้ (ตัวอย่างเช่น ข้อมูลที่เป็นตัวเลข)
Fibonacci Search
Fibonacci Search [13] เป็นเทคนิคการค้นหาที่ใช้จำนวน Fibonacci ในการหาข้อมูลที่มีอยู่ใน Array ที่เรียงลำดับแล้ว
ลักษณะการทำงานนี้จะคล้ายกันกับ Binary Search โดย
- เป็นเทคนิคที่ต้องแบ่งข้อมูลเสียก่อน (Divide and Conquer)
- และมี Time Complexity เท่ากับ O(log n)
อย่างไรก็ดี เทคนิคนี้มีข้อแตกต่าง ได้แก่
- Fibonacci Search แบ่งข้อมูลในอัตราส่วนที่ไม่เท่ากัน ผิดกับ Binary Search ที่แบ่งข้อมูลเป็นครึ่งต่อครึ่ง
- Fibonacci Search ใช้ Operator เป็น + กับ – แต่ Binary Search ใช้การหารซึ่งอาจจะส่งผลกระทบต่อเครื่องที่มี CPU ที่ไม่แรงพอ
- และเทคนิคนี้เหมาะกับข้อมูลที่มีขนาดใหญ่ที่ไม่สามารถใส่ใน CPU cache หรือ RAM ได้อย่างเพียงพอ
ขั้นตอนการทำงาน
เราสามารถสรุปการทำงานได้ตามตัวอย่างด้านล่างนี้
ขั้นตอนแรก เรากำหนดให้ F0 = 0, F1 = 1 และ F2 = 1 แล้วเพิ่มจำนวน Fibonacci ได้เรื่อย ๆ โดยให้ค่า F0 = F1, F1 = F2 และ F2 = F0 + F1 จนกว่าค่า F2 จะมีค่ามากกว่าขนาดของ Array (ในที่นี้ใช้ size)
โดยในตัวอย่างจะเป็น Array ที่ข้อมูลทั้งหมด 9 ข้อมูล ดังนั้น ผลลัพธ์ที่ได้จากการคำนวณ Fibonacci จะได้ F0 = 5 F1 = 8 และ F2 = 13

เมื่อจบขั้นตอนแรกแล้ว เรากำหนดให้ค่าที่เป็นจุดเริ่มต้น (start) = -1
จากนั้นเราใช้สูตรคำนวณเพื่อหาตำแหน่งและเช็คว่าตำแหน่งนั้นเป็นค่าที่เราต้องการหรือไม่ โดย
ตำแหน่งที่ต้องการหา (Index ที่ต้องการหา) = min(start + F0, size – 1)
ในตัวอย่าง เราแทนค่าลงไป ได้เป็น
= min(-1 + 5, 9 – 1)
= min(4, 8)
= 4
จากคำตอบ เราจะได้ตำแหน่ง index ใน Array นั้นที่เท่ากับ 4 โดยค่าที่ได้ในตำแหน่งนั้นมีค่าเท่ากับ 5 ซึ่งมีค่ามากกว่าค่าที่ต้องการ

เมื่อเราทราบว่าค่าที่เจอนั้นมีค่ามากกว่าค่าที่ต้องการ กรณีนี้ เราจะกำหนดให้
- F2 = F0
- F1 = F1 – F0
- และ F0 = F2 – F1
โดยในตัวอย่างแทนค่าได้เป็น
- F2 = 5
- F1 = 8 – 5 = 3
- และ F0 = 5 – 3 = 2

จากนั้นให้นำไปแทนค่าในฟังก์ชัน min(start + F0, size – 1) เพื่อหา Index ที่หาอีกเช่นเคย โดยจะได้ค่าเท่ากับ 1 ซึ่งมีค่าในตำแหน่งนั้นใน Array เท่ากับ 2 ซึ่งมีค่าน้อยกว่าค่าที่เราต้องการหา

หลังจากที่ทราบว่าค่าที่เราพบมีค่าน้อยกว่าค่าที่เราต้องการหา ให้เรากำหนดค่า
- F2 = F1
- F1 = F0
- F0 = F2 – F1
- และค่าเริ่มต้น (start) เท่ากับ 1
เราแทนค่าจะได้เป็น
- F2 = 3
- F1 = 2
- และ F0 = 3 – 2 = 1
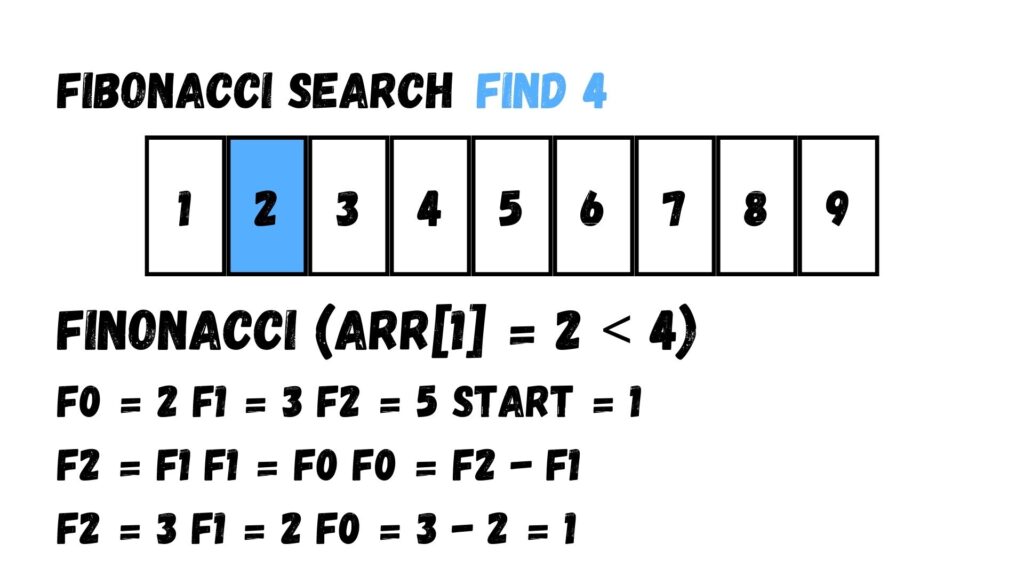
เรานำผลที่ได้จากการคำนวณในขั้นตอนก่อนหน้ามาแทนที่ในฟังก์ชัน min เพื่อหาตำแหน่งอีกเช่นเคย โดยเราจะได้ index เท่ากับ 2 ที่มีค่าเท่ากับ 3
ค่าที่เราค้นหาได้ค่านั้น มีค่าน้อยกว่าค่าที่เราต้องการ

หลังจากที่ทราบว่าค่าที่พบน้อยกว่าค่าที่เราต้องการ ให้เราปรับค่า F0, F1 และ F2 โดยแทนค่าแล้วจะได้ F2 = 2 F1 = 1 F0 = 2 – 1 = 1 ร่วมกับกำหนดค่า start เท่ากับ 2
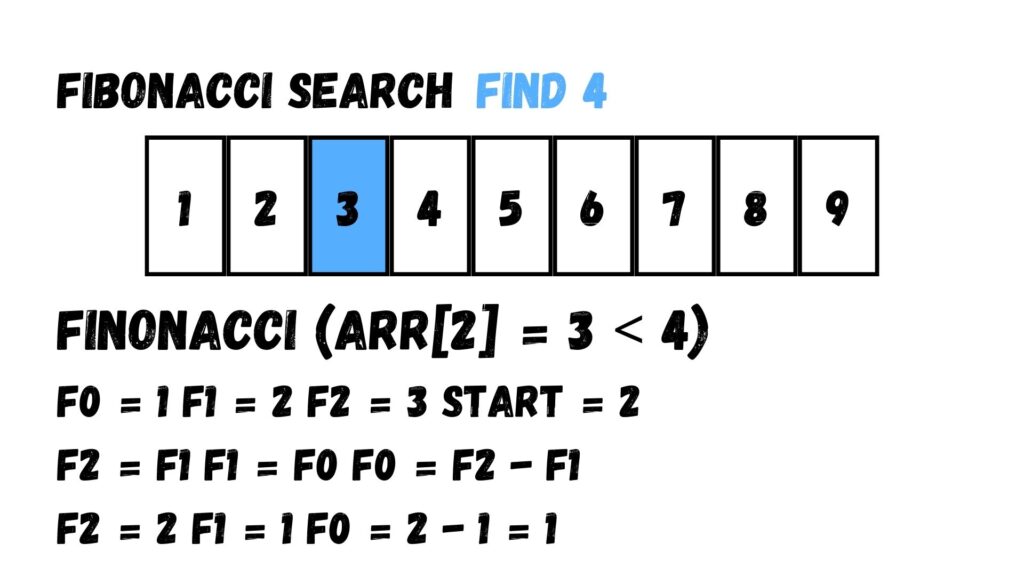
เรานำค่าที่ได้ F0, F1, F2 และ start มาแทนค่าในฟังก์ชัน min แล้วเราจะได้ค่า Index เท่ากับ 3 ซึ่งมีค่าเท่ากับ 4 ตามที่เราต้องการ

เราเขียนโค้ดได้ตามด้านล่างนี้
def fibonacci_search(arr, find):
f0, f1, f2 = 0, 1, 1
start = -1
size = len(arr) - 1
while f2 < size:
f0 = f1
f1 = f2
f2 = f0 + f1
while f2 > 1:
pos = min(start + f0, size)
if find > arr[pos]:
f2 = f1
f1 = f0
f0 = f2 - f1
start = pos
elif find < arr[pos]:
f2 = f0
f1 = f1 - f0
f0 = f2 - f1
else:
return pos
return -1Algorithm นี้มีประสิทธิภาพการทำงานตามระยะเวลาการทำงาน (Time Complexity) เท่ากับ O(log n) และมี Space Complexity เท่ากับ O(1)
เทคนิคนี้เป็นเทคนิคที่ดี อย่างไรก็ตาม Fibonacci Search มีข้อจำกัด ได้แก่
- ต้องใช้กับ Array ที่ Sorted แล้วเท่านั้น
- การคำนวณค่า Fibonacci มีค่าที่ซับซ้อน ส่งผลให้ทำงานได้ช้ากรณีที่ข้อมูลที่มีขนาดใหญ่มาก
- ค่าที่คำนวณได้จาก Fibonacci จะมีค่าเพิ่มขึ้นแบบ Exponential ส่งผลให้ค่าเกินกว่าข้อจำกัดของตัวแปร Integer ส่งผลให้เกิดข้อผิดพลาดได้
จากข้อจำกัดตามข้างบนนี้ ส่งผลให้ Fibonacci ไม่ค่อยเหมาะสมต่อการนำไปใช้งานจริงเท่าไรนัก
Sorting Algorithm
Sorting Algorithm เป็น Algorithm ที่ใช้ในการเรียงลำดับของข้อมูลใน Array ที่เป็นตัวเลข กับตัวอักษรให้เป็นไปตามลำดับที่กำหนด โดยจำเป็นต้องเรียงลำดับได้อย่างมีประสิทธิภาพ [14]
ตัวอย่างของเทคนิค Sorting Algorithm ได้แก่ Selection Sort, Bubble Sort, Insertion Sort, Heap Sort, Merge Sort และ Quick Sort
Selection Sort
Selection Sort [14, 15] เป็น Algorithm สำหรับการเรียงลำดับข้อมูลอย่างง่าย และมีประสิทธิภาพโดยการเลือกตัวเลขที่มีค่าน้อยที่สุด (หรือมากที่สุด) ใน Array นั้น แล้วย้ายข้อมูลไปยังด้านซ้าย หรือด้านขวาสุดของ Array ตามลำดับ
ขั้นตอนการทำงาน
เราแสดงได้ตามภาพเป็นขั้นตอนตามด้านล่างนี้
ขั้นแรก ให้เลือกค่าที่น้อยที่สุดใน Array ตั้งแต่ Index ที่ 0 ไปจนถึงขอบด้านขวาสุดของ Array เราจะได้ค่าที่น้อยที่สุดคือ 11 ให้เรานำค่านี้สลับกับตัวเลขใน Index 0 (64)

ต่อมา เลือกค่าที่น้อยที่สุดใน Array ตั้งแต่ Index ที่ 1 เป็นต้นไป เราจะได้ค่าที่น้อยที่สุดคือ 12 ให้เรานำค่าสลับกับตัวเลขใน Index ที่ 1 (25)
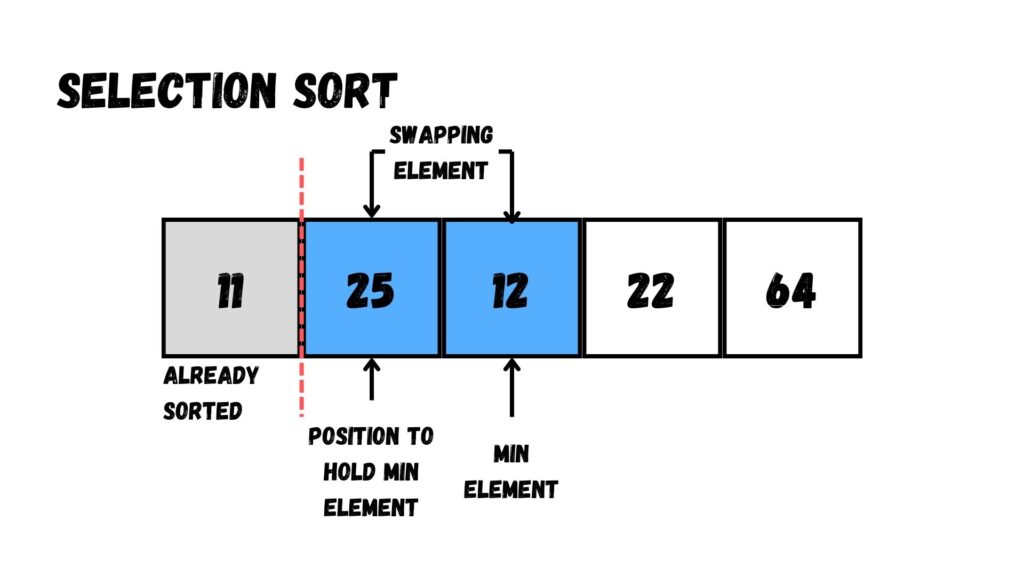
ขั้นตอนที่สาม ให้เลือกค่าที่น้อยที่สุดใน Array ตั้งแต่ Index ที่ 2 ไปจนถึงด้านขวาสุด เราจะได้ค่าที่น้อยที่สุดคือ 22 ให้เราสลับกับตัวเลขใน Index ที่ 2 (25)
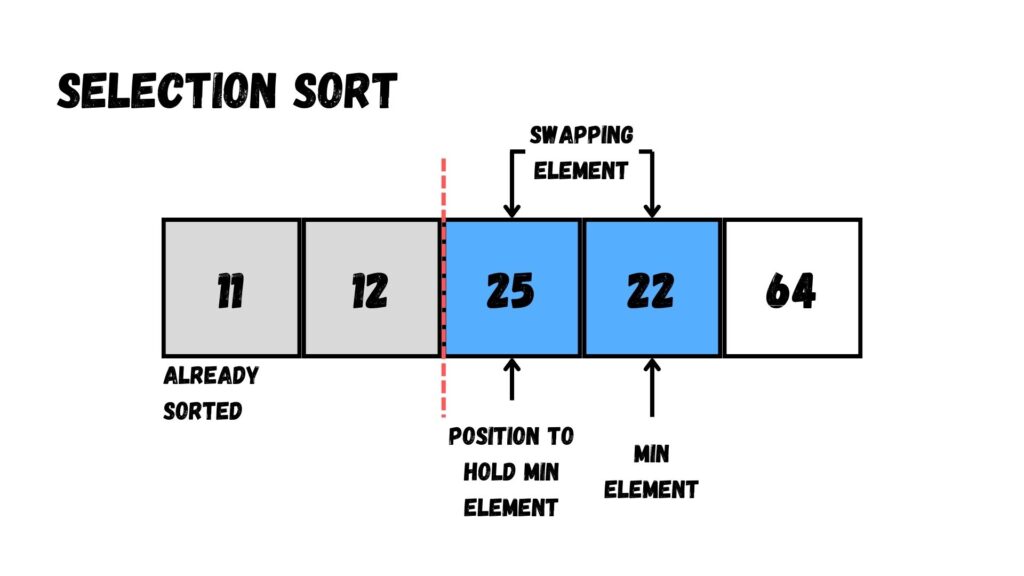
หลังจากนั้น เราจะไม่พบค่าที่น้อยที่สุด
เมื่อไม่พบค่าที่น้อยที่สุด เราก็ไม่ต้องสลับค่ากับตัวเลขที่เหลือใน Array
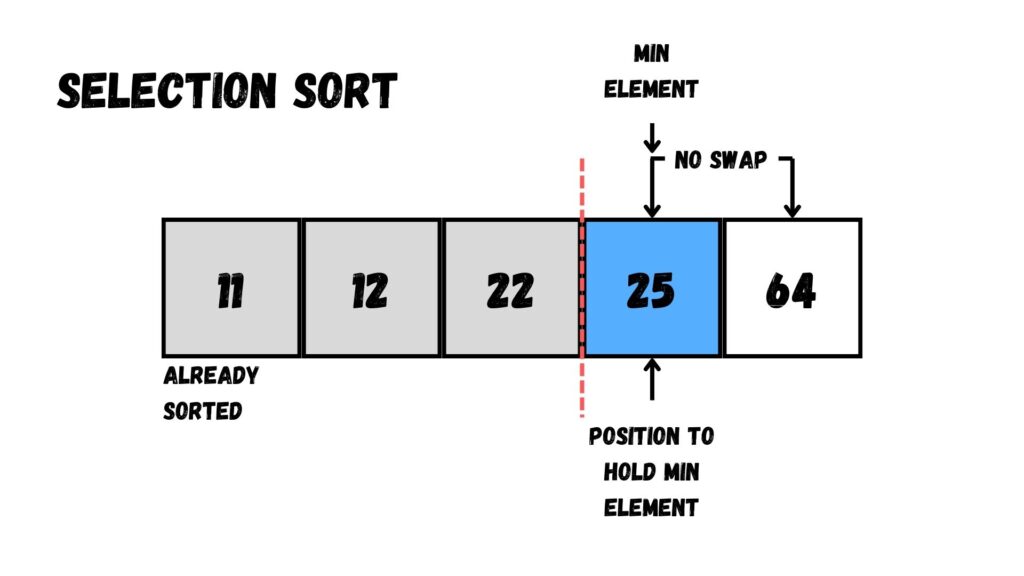
ดังนั้นแล้ว เราจะได้ Array ที่เรียงข้อมูลเสร็จเรียบร้อยตามด้านล่างนี้
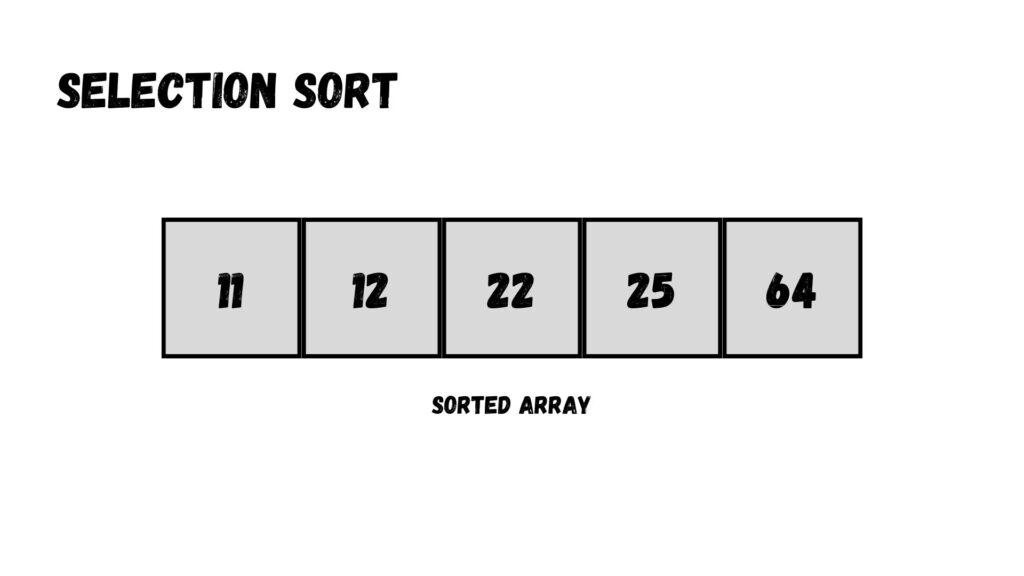
เราสามารถเขียนโค้ดได้ตามด้านล่างนี้
def selection_sort(arr):
for i in range(0, len(arr) - 1):
minimum = -1
for j in range(i, len(arr)):
if j == i:
minimum = j
if arr[j] < arr[minimum]:
minimum = j
if arr[minimum] < arr[i]:
arr[minimum], arr[i] = arr[i], arr[minimum]
return arrAlgorithm นี้มีประสิทธิภาพการทำงานตามระยะเวลาการทำงาน (Time Complexity) เท่ากับ O(N^2) และมี Space Complexity เท่ากับ O(1)
จากการวิเคราะห์ Time Complexity แล้ว Algorithm นี้ที่เป็น Algorithm ที่ใช้เวลามาก ไม่เหมาะกับข้อมูลที่มีขนาดใหญ่ แต่ Algorithm นี้่มีข้อดี ได้แก่
- เป็น Algorithm ที่เข้าใจได้ง่าย
- และทำงานได้ดีกับข้อมูลที่มีขนาดเล็ก
Bubble Sort
Bubble Sort [14, 16] เป็นเทคนิคการเรียงข้อมูลอย่างง่ายที่สุด โดยเปรียบเทียบข้อมูลสองตำแหน่งที่ติดกัน
กรณีที่ข้อมูลทีอยู่ทางด้านซ้ายมีค่ามากกว่า ให้เราสลับค่ากัน โดยย้ายข้อมูลที่มีค่ามากกว่าไปทางขวา จากนั้น เราเปรียบเทียบ และสลับค่าที่อยู่ด้านขวานั้น ไปเรื่อย ๆ จนถึงคู่สุดท้าย
ขั้นตอนการทำงาน
เราแสดงได้ตามขั้นตอนตามด้านล่างนี้
ขั้นตอนแรก เรานำข้อมูลคู่แรก ระหว่าง 64 กับ 25 มาเปรียบเทียบ ว่าค่าไหนที่มีค่ามากกว่ากัน โดยเราจะพบว่าค่า 64 มากกว่า 25 ให้เราสลับค่าเพื่อย้ายค่า 64 ไปทางขวา
เมื่อย้ายไปแล้ว ให้เราจับคู่กับเลขที่อยู่ข้างขวาแบบเดียวกันกับขั้นตอนก่อนหน้า เพื่อดูว่าตัวไหนมากกว่ากันแล้วให้สลับค่าที่มากกว่าไปอยู่ด้านขวา เราทำแบบนี้ไปเรื่อย ๆ จนกว่าจะถึงคู่สุดท้ายที่
- ค่าที่เราสลับมามีค่าน้อยกว่า
- หรืออยู่ขอบทางด้านขวาของ Array

เมื่อเราจับคู่ และสลับค่าในรอบแรกเสร็จแล้ว
ต่อมา เราให้เราทำค่าในคู่ที่สองระหว่าง 25 กับ 12 มาเปรียบเทียบดูว่าตัวไหนมากกว่ากัน แล้วสลับค่าที่มากกว่าไปด้านขวา

หลังจากนั้น ให้เราทำซ้ำแบบเดิมไปจนกว่าจะเรียงข้อมูลสำเร็จเรียบร้อย


เราสามารถเขียนโค้ดได้ตามด้านล่างนี้
def bubble_sort(arr):
for i in range(len(arr)):
for j in range(len(arr) - i - 1):
if arr[j] > arr[j+1]:
arr[j+1], arr[j] = arr[j], arr[j+1]
return arrAlgorithm นี้มีประสิทธิภาพการทำงานตามระยะเวลาการทำงาน (Time Complexity) เท่ากับ O(N^2) และมี Auxiliary Space เท่ากับ O(1)
จากการวิเคราะห์ Time Complexity แล้ว เราจะพบว่าเทคนิคนี้ใช้เวลามาก ไม่เหมาะกับข้อมูลที่มีขนาดใหญ่
อย่างไรก็ดี Algorithm นี้มีข้อดี คือ เป็น Algorithm ที่เข้าใจได้ง่าย และไม่ต้องการ RAM เพิ่มเติม
Insertion Sort
Insertion Sort [14, 17] เป็นเทคนิคการเรียงข้อมูลอย่างง่ายที่มีลักษณะคล้ายกับการเรียงไพ่ในมือ โดยจะแบ่งระหว่าง Array ที่เรียงข้อมูลแล้ว และ Array ที่ไม่ได้เรียงข้อมูล โดยเรานำค่าจากข้อมูลที่ยังไม่ได้เรียงข้อมูลตามลำดับ (Sorted) มาแทรกไว้ในตำแหน่งที่ถูกต้อง
ขั้นตอนการทำงาน
เราแสดงได้ตามขั้นตอนตามด้านล่างนี้
ขั้นตอนแรก เรามองหาตัวเลขที่อยู่ตำแหน่งที่ไม่ถูกต้อง โดยเปรียบเทียบระหว่างตัวเลขในลำดับ Array ปัจจุบัน (25) กับ Array ในลำดับก่อนหน้า (64) ว่าค่าใน Array ปัจจุบันมีค่าน้อยกว่าค่าก่อนหน้าหรือไม่ เราจะพบว่า 25 มีค่าน้อยกว่า 64 ให้เราสลับค่า นำ 25 ไปอยู่ทางด้านหน้าของค่า 64
ต่อมา เรามองหาตัวเลขที่อยู่ในตำแหน่งที่ไม่ถูกต้องต่อมาคือเลข 12 ค่านี้เราจะเปรียบเทียบกับ Array ในลำดับก่อนหน้า (64 และ 25) ว่ามีค่าน้อยกว่าหรือไม่ เราจะพบว่าค่า 12 มีค่าน้อยกว่าทั้ง 64 และ 25 ให้เราสลับค่าไปจนถึงทางด้านหน้าสุดของ Array
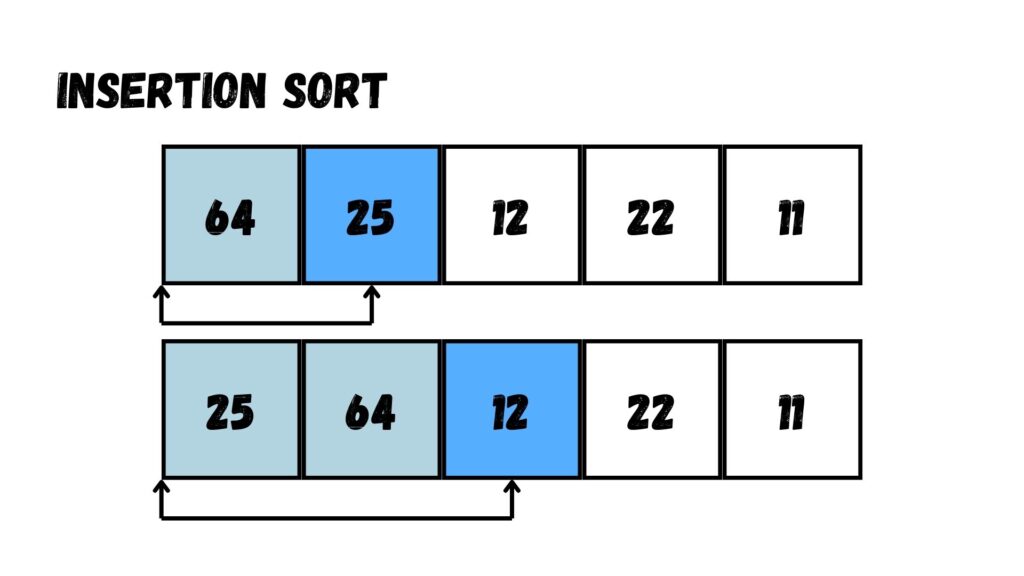
ขั้นตอนที่สาม เรามองหาค่าที่ไม่ถูกต้องอีกเช่นกัน คือ 22 โดยเปรียบเทียบกับค่าก่อนหน้า (64, 25 และ 12) แล้วเราจะพบว่าค่า 22 น้อยกว่า 64 และ 25 แต่ไม่น้อยกว่า 12
ดังนั้น เราจะสลับค่ากันกับ 64 และ 25 เพื่อให้ค่า 22 อยู่ด้านหน้าสองค่านี้ แต่อยู่หลัง 12
ขั้นตอนที่สี่ เรามองหาค่าที่ไม่ถูกเช่นกัน คือ 11 โดยเปรียบเทียบกับค่าก่อนหน้า (64, 25, 22 และ 12) แล้วเราพบว่าค่า 11 น้อยกว่าทุกตัว
ดังนั้น เราจะสลับกับ 64, 25, 22 และ 12 เพื่อให้ค่า 11 อยู่ด้านซ้ายสุด
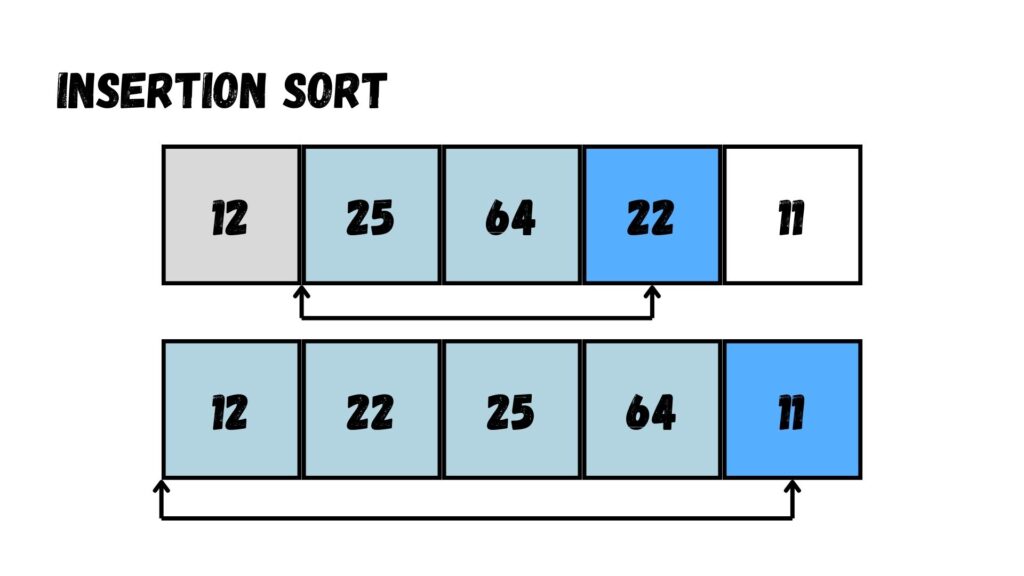
เมื่อทำเสร็จแล้ว ค่าตัวเลขที่อยู่ใน Array จะเรียงลำดับจากน้อยไปมากตามภาพด้านล่างนี้

เราสามารถเขียนโค้ดได้ตามด้านล่างนี้
def insertion_sort(arr):
size = len(arr)
for i in range(size):
if arr[i] >= arr[i-1]:
continue
for j in range(i, 0, -1):
if arr[j] < arr[j-1]:
arr[j-1], arr[j] = arr[j], arr[j-1]
return arrAlgorithm นี้มีประสิทธิภาพการทำงานตามระยะเวลาการทำงาน (Time Complexity) ในกรณีที่เป็น
- Worst Case กับ Average Case จะมีค่าเท่ากับ O(N^2)
- Best Case มีค่าเท่ากับ O(N)
และมี Auxiliary Space เท่ากับ O(1)
Algorithm นี้มีข้อดีคือใช้ง่าย เหมาะกับข้อมูลที่มีขนาดเล็ก และผ่านการเรียงลำดับมาก่อนหน้าแล้ว
อย่างไรก็ดี Algorithm นี้ใช้เวลามาก ไม่เหมาะกับข้อมูลที่มีขนาดใหญ่ ตามที่วิเคราะห์ใน Time Complexity
Heap Sort
Heap Sort [14, 18] เป็นการเรียงข้อมูลใน Array โดยอาศัยหลักฐานของ Binary Heap [19] มาเป็นกระบวนการหลักในการทำงาน
ข้อดีของการใช้ Binary Heap คือทำงานได้เร็วกว่าการใช้ Vector หรือการเก็บข้อมูลแบบ Array ยาว ๆ ที่ต้องใช้ระยะเวลาในการจัดการข้อมูลมาก โดย Binary Heap มีส่วนประกอบทั้งหมด 3 ส่วน ได้แก่
- Root ที่เป็นโหนดที่อยู่ชั้นบนสุด
- Parent คือโหนดที่อยู่เหนือกว่าโหนดที่อยู่ด้านล่าง
- และ Child เป็นโหนดที่อยู่ด้านล่าง
โดยโหนดในแต่ละระดับของ Binary Heap จะแตกเป็นสองสาขา ซ้าย และขวา โดยเราจะต้องเติมจากทางซ้ายก่อน แล้วไปเติมทางขวาจนเติม จากนั้นค่อยเพิ่มระดับใหม่ลงไปอีกระดับหนึ่ง
การแบ่งประเภทของ Binary Heap มีสองประเภท ได้แก่
- Max Heap ที่ให้โหนด Parent มีค่ามากกว่าโหนด Child และโหนดที่อยู่ระดับ Root มีค่ามากที่สุด
- Min Heap ที่ให้โหนด Parent มีค่าน้อยกว่าโหนด Child และโหนดที่อยู่ระดับ Root มีค่าน้อยที่สุด
การจัดข้อมูลใน Binary Heap เราทำได้โดยการเก็บข้อมูลใน Array ที่มีข้อแตกต่างกับการเก็บใน Array ปกติ โดยโหนด Child ของ Parent จะเก็บที่ 2 x (parent index) + 1 กับ 2 x (parent index) + 2 ทางด้านซ้าย และขวา ตามลำดับ
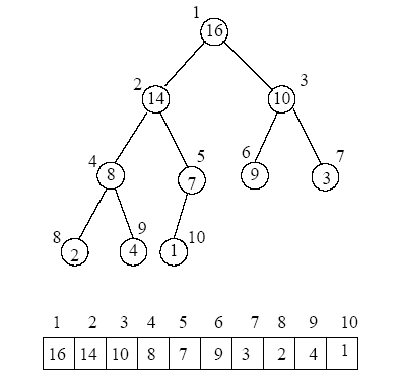
ต่อมา เรามาเข้าเรื่อง Heap Sort
ขั้นตอนการทำงาน
เราแสดงได้ตามขั้นตอนตามด้านล่างนี้
ขั้นแรก เราแปลงข้อมูลจาก Array ให้เป็น Binary Heap ที่เป็น Max Heap เสียก่อน แต่จากภาพ ข้อมูลเป็นไปตาม Max Heap อยู่แล้ว เราจึงไม่ต้องทำอะไรเพิ่ม

ขั้นต่อมา เราสลับเอาโหนดที่อยู่บนสุด (Root Element) ย้ายไปทางขวาสุดของ Array แล้วนำโหนดที่อยู่ตำแหน่งสุดท้ายของ Heap (= 11) ไปไว้บริเวณโหนด Root ที่เสมือนกับการนำข้อมูลออกจากโหนดใน Binary Heap

ถัดจากนั้น เรานำข้อมูลใน Root มาเปรียบเทียบกับค่าในโหนด Child (25, 12, และ 22) แล้วสลับค่า ให้ค่าที่มากกว่าย้ายมาอยู่บนโหนด Parent กับ Root แทน จนกระทั่งกลายเป็น Max Heap
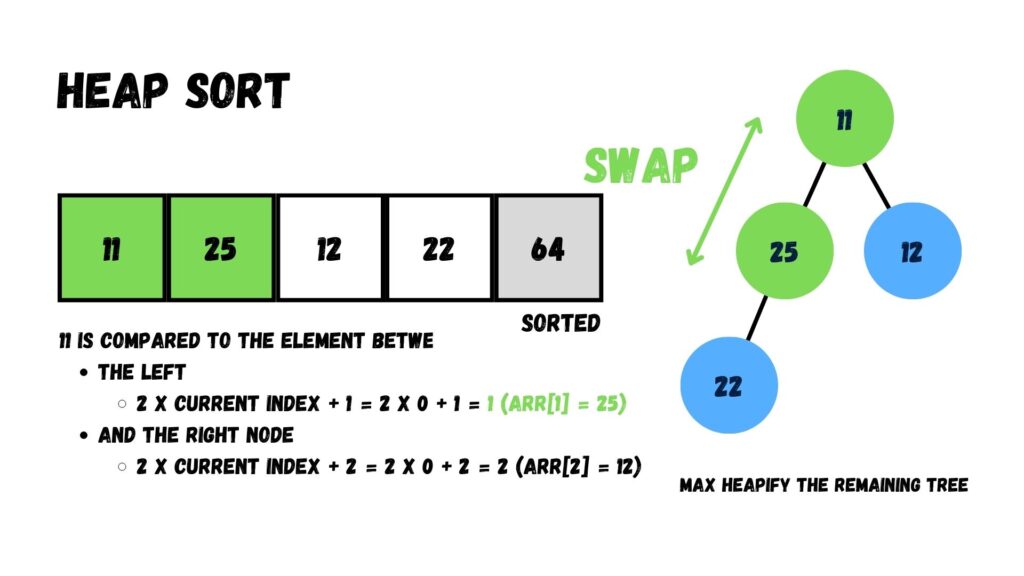
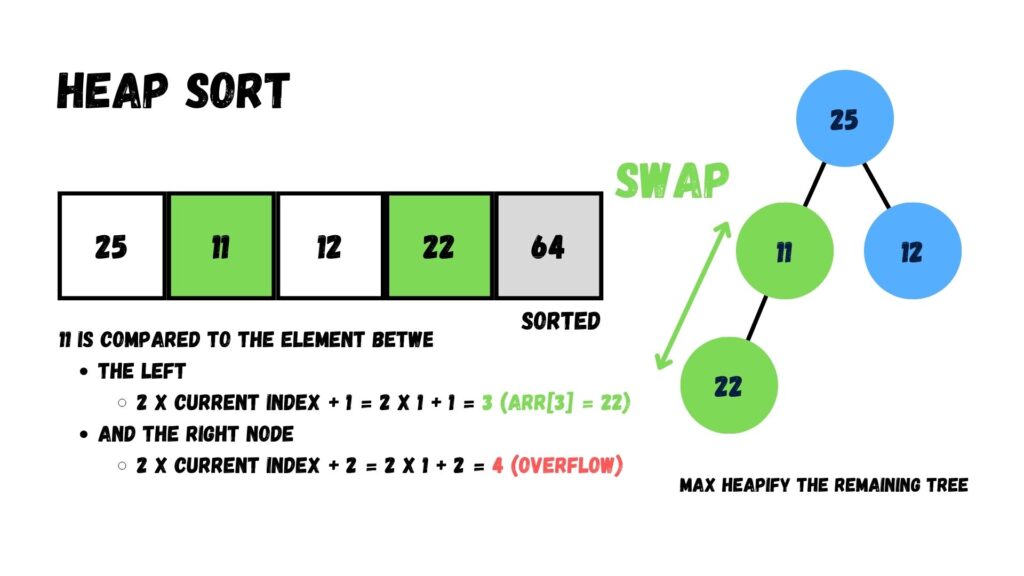
เมื่อทำเสร็จแล้ว ให้เรานำค่าที่อยู่บน Root (= 25) ย้ายออกจาก Heap โดยย้ายไปอยู่ทางด้านขวาสุดของ Array แล้วนำค่าที่อยู่โหนดสุดท้าย (= 11) ไปไว้ที่ Root

จากภาพ เราจะเหลือข้อมูลที่นำมาทำ Max Heap ทั้งหมด 3 อัน ได้แก่ 11, 22 และ 12 ให้เรานำค่าใน Root มาเปรียบเทียบกับที่เหลือ โดยให้ค่าที่มากกว่าอยู่ระดับเหนือกว่าค่าที่น้อยกว่า
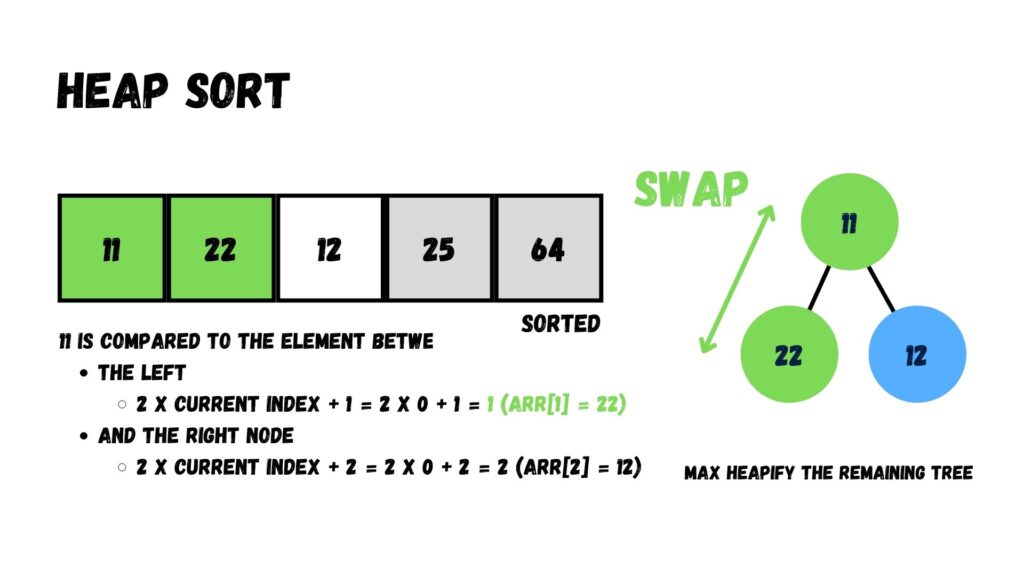
เมื่อสลับเสร็จแล้ว เรานำค่าที่อยู่บน Root (22) ออกจาก Heap โดยย้ายไปทางด้านหลังของ Array เพื่อสลับกันระหว่าง 22 กับ 12
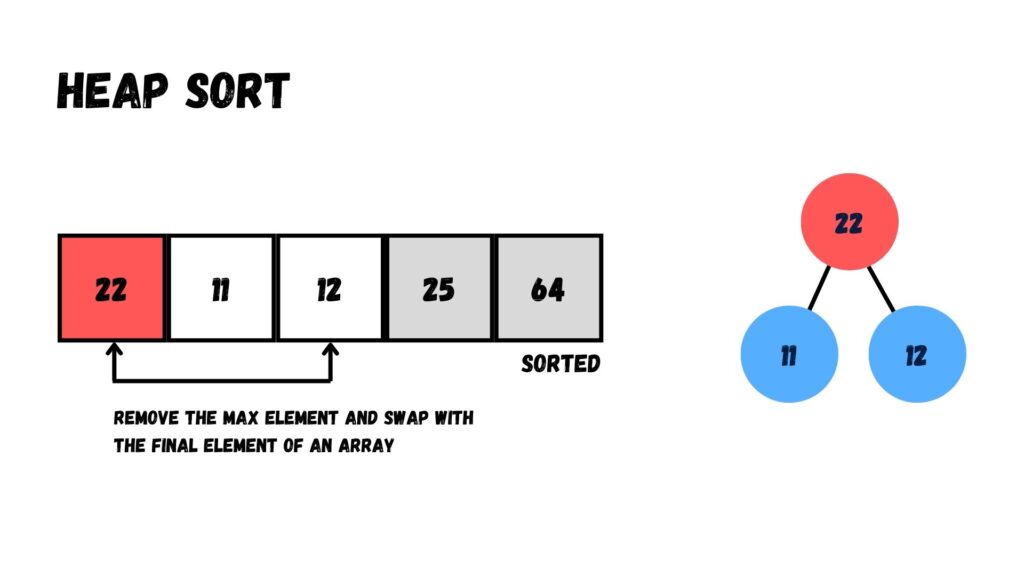
ตอนนี้จะเหลืออยู่ 2 ค่า ได้แก่ 12 กับ 11 โดยจากภาพเป็น Max Heap เนื่องมาจากค่าที่มากกว่า (12) อยู่ระดับบน ส่วนค่าที่น้อยกว่า (11) อยู่ระดับล่าง
เราไม่จำเป็นต้องย้ายข้อมูลเพิ่ม เพียงแค่นำค่าที่อยู่บน Root (= 12) ออกจาก Heap แล้วย้ายไปทางด้านหลังของ Array โดยสลับกับค่าที่อยู่โหนดสุดท้ายของ Heap (= 11)
เมื่อย้ายเสร็จแล้ว เราจะเหลือข้อมูล 1 ค่า คือ 11 ซึ่งไม่มีค่าอื่นให้เปรียบเทียบแล้ว
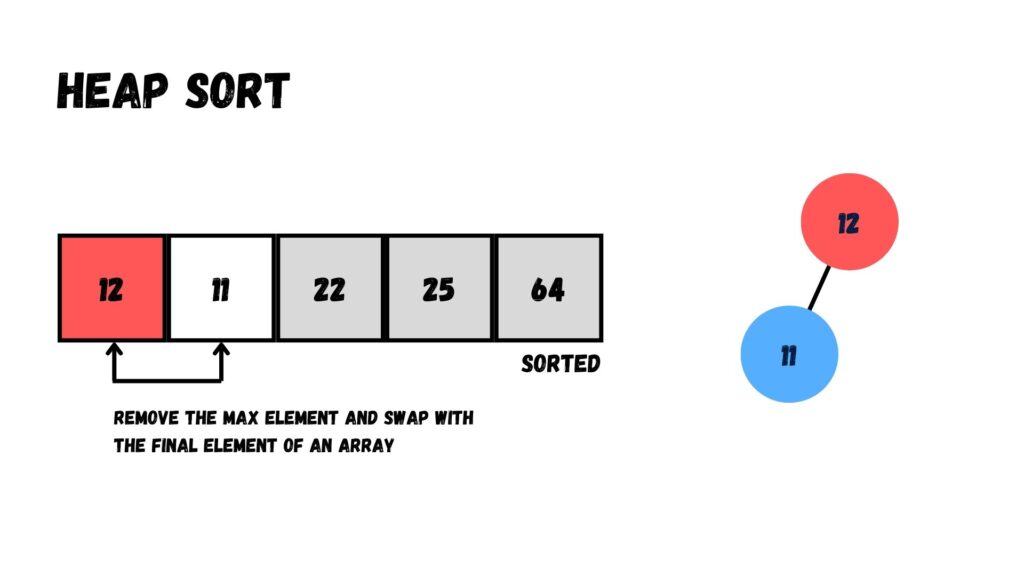
ผลลัพธ์ที่ได้คือ Array ที่ผ่านการเรียงข้อมูลเรียบร้อย

เราสามารถเขียนโค้ดได้ตามด้านล่างนี้
def heapify(arr, low, high, i = 0):
largest = i
left = 2 * i + 1
right = 2 * i + 2
if left < high and arr[left] > arr[i]:
largest = left
if right < high and arr[right] > arr[largest]:
largest = right
if largest != i:
arr[largest], arr[i] = arr[i], arr[largest]
arr = heapify(arr, 0, high, largest)
return arr
def heap_sort(arr):
size = len(arr)
# build a heap
start = size // 2 - 1
for i in range(start, -1, -1):
arr = heapify(arr, 0, size, i)
# Swap inside heap
for i in range(size-1, -1, -1):
arr[i], arr[0] = arr[0], arr[i]
arr = heapify(arr, 0, i)
return arrAlgorithm นี้มีประสิทธิภาพการทำงานตามระยะเวลาการทำงาน (Time Complexity) เท่ากับ O(n log n) และมี Auxiliary Space เท่ากับ O(1) ในกรณีที่ใช้วนลูป แต่ถ้าเป็นแบบ Recursion จะมีค่าเท่ากับ O(log n)
Algorithm นี้มีข้อดีคือทำงานได้เร็ว มีประสิทธิภาพ ใช้หน่วยความจำน้อย และเรียบง่าย อย่างไรก็ดี เทคนิคนี้ทำงานไม่ดีนักในกรณีที่ข้อมูลใน Array ซับซ้อน
Merge Sort
Merge Sort [14, 20, 21] เป็นเทคนิคการเรียงข้อมูลโดยแบ่ง Array เป็น Array ที่มีขนาดเล็ก แล้วนำ Array ที่มีขนาดเล็กมาเรียงข้อมูล จากนั้นนำ Array มารวมกันให้เป็น Array เดียวที่ผ่านการเรียงข้อมูลแล้ว
ฟังดูไม่เห็นภาพ เรามาดูขั้นตอนการทำงานจะดีกว่า
ขั้นตอนการทำงาน
เราแสดงได้ตามขั้นตอนตามด้านล่างนี้ โดยในตัวอย่างนี้เราจะใช้ Array ที่มีข้อมูลทั้งหมด 4 ข้อมูล ได้แก่ 64, 25, 12 และ 22
ขั้นตอนแรก เราแบ่งข้อมูลออกเป็นครึ่งหนึ่งเสียก่อน โดยแบ่งเป็น Array ละ 2 ข้อมูล
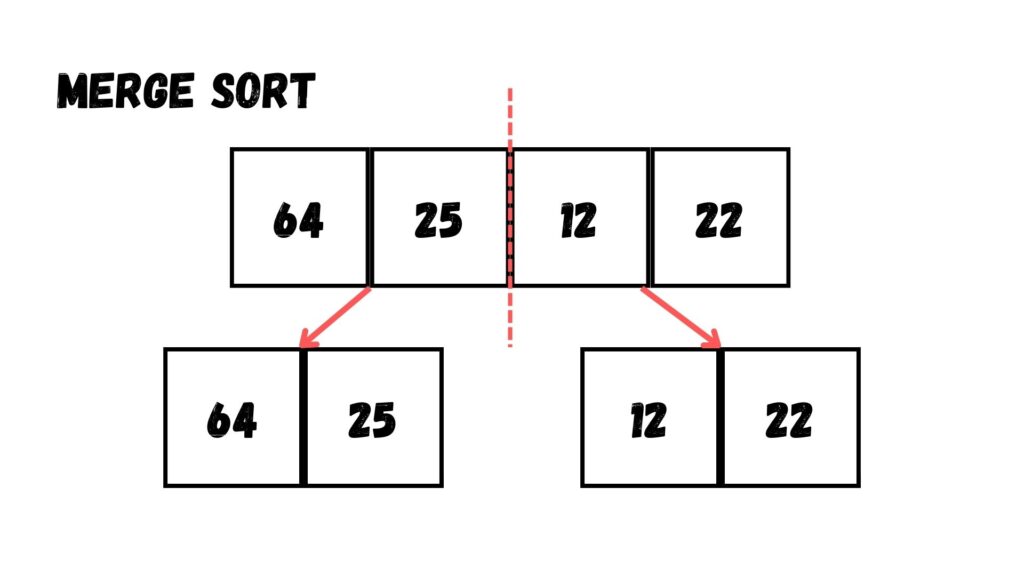
จากนั้น เราก็แบ่งข้อมูลไปอีกครึ่งหนึ่ง ให้เหลือ Array ละ 1 ข้อมูล
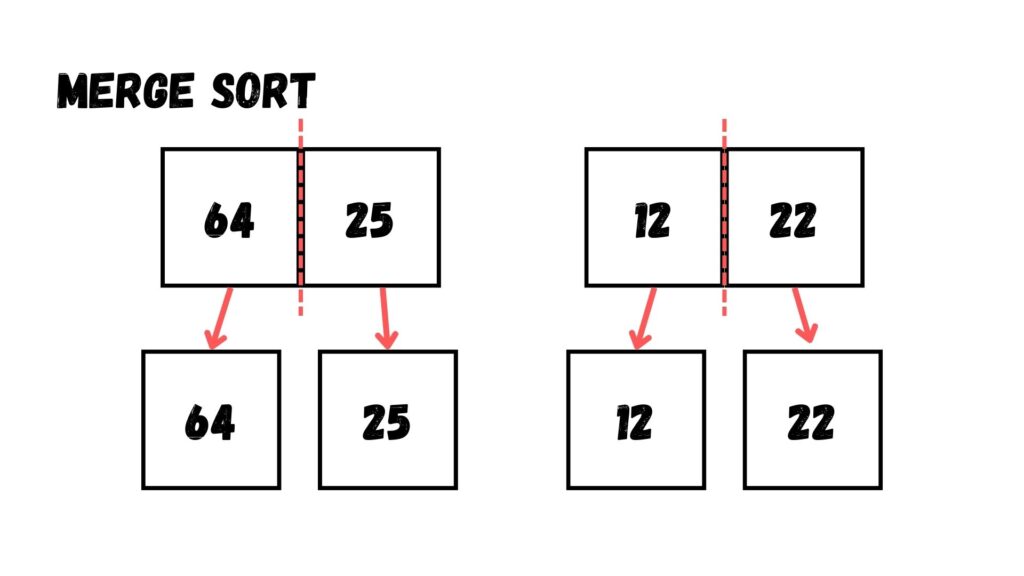
เมื่อเราแบ่งข้อมูลจนเหลือ Array 1 ข้อมูลแล้ว ให้เรารวม Array
เวลาที่เรารวมข้อมูลลงไปใน Array เดียวกันให้เราเทียบข้อมูลระหว่าง 2 Array โดยให้ค่าที่น้อยกว่าอยู่ก่อน และค่าที่มากกว่าอยู่หลัง จนกว่าจะรวมถึงเป็น Array เดียว
ผลลัพธ์ที่ได้ก็จะได้เป็น Array ที่ผ่านการเรียงข้อมูลเรียบร้อยแล้ว


เราสามารถเขียนโค้ดได้ตามด้านล่างนี้
def merge_sort(arr):
overall_size = len(arr)
if overall_size == 1:
return arr
mid_arr = (overall_size) // 2
left = merge_sort(arr[:mid_arr])
right = merge_sort(arr[mid_arr:])
size_left, size_right = len(left), len(right)
i, j = 0, 0
target_arr = []
while i < size_left and j < size_right:
if left[i] <= right[j]:
target_arr.append(left[i])
i += 1
else:
target_arr.append(right[j])
j += 1
for i_left in range(i, size_left):
target_arr.append(left[i_left])
for i_left in range(j, size_right):
target_arr.append(right[i_left])
return target_arrAlgorithm นี้มีประสิทธิภาพการทำงานตามระยะเวลาการทำงาน (Time Complexity) เท่ากับ O(n log n)
และมี Auxiliary Space เท่ากับ O(N) เนื่องมาจากขั้นตอนการเรียงข้อมูลใน Merge Sort จำเป็นต้องก็อบปี้ข้อมูลลงไปใน Array ที่ช่วยสำหรับการเรียงข้อมูล (Auxiliary Array) ที่ต้องใช้หน่วยความจำในการเก็บตัวแปรดังกล่าว
Algorithm นี้มีข้อดีได้แก่
- ทำงานได้เร็ว
- การันตีประสิทธิภาพเมื่อเกิด Worst Case ที่ O(n log n)
- เหมาะสมต่อการเรียงข้อมูลใน Dataset ที่มีขนาดใหญ่
- ทำงานแบบ Parallel ได้
อย่างไรก็ดี เทคนิคนี้มีข้อด้อย ได้แก่
- ต้องใช้หน่วยความจำเพิ่มเติมสำหรับการเก็บข้อมูล Auxiliary Array ในขั้นตอนการเรียงข้อมูล
- ไม่ได้แทนที่ค่าลงไปใน Array นั้น ๆ เลย (ไม่เป็น in-place)
- ทำงานได้ช้าในกรณีที่ Array มีขนาดเล็กเมื่อเทียบกับ Insertion Sort
Quick Sort
Quick Sort [14, 22, 23] เป็นเทคนิคการเรียงข้อมูลโดยการเลือกข้อมูลใน Array ข้อมูลหนึ่งเป็น Pivot แล้วจัดข้อมูลที่มีค่าน้อยกว่าอยู่ทางซ้าย และค่ามากกว่าอยู่ทางขวา แล้วแบ่ง Array รอบ ๆ ค่า Pivot นั้น
ขั้นตอนการทำงาน
เราแสดงได้ตามขั้นตอนตามด้านล่างนี้
ขั้นแรก เราเลือกค่าใดค่าหนึ่งใน Array ให้เป็นค่า Pivot เสียก่อน โดยเราสามารถเลือกค่า Pivot จาก
- ข้อมูลแรกใน Array
- ข้อมูลในตำแหน่งหลังสุดของ Array
- การเลือกแบบสุ่ม
- เลือกตรงกลางของ Array
ในที่นี้เราเลือกข้อมูลที่อยู่ทางขวาสุด
ต่อมา เรากำหนดค่า i ที่เป็นค่าตำแหน่งข้อมูลใน Array สำหรับการสลับตำแหน่งกับข้อมูลที่มีค่าน้อยกว่าหรือเท่ากับ Pivot โดยเรากำหนดค่าเริ่มต้นที่ -1 (ก็คือตำแหน่งถัดจากตำแหน่งซ้ายสุดของ Array)
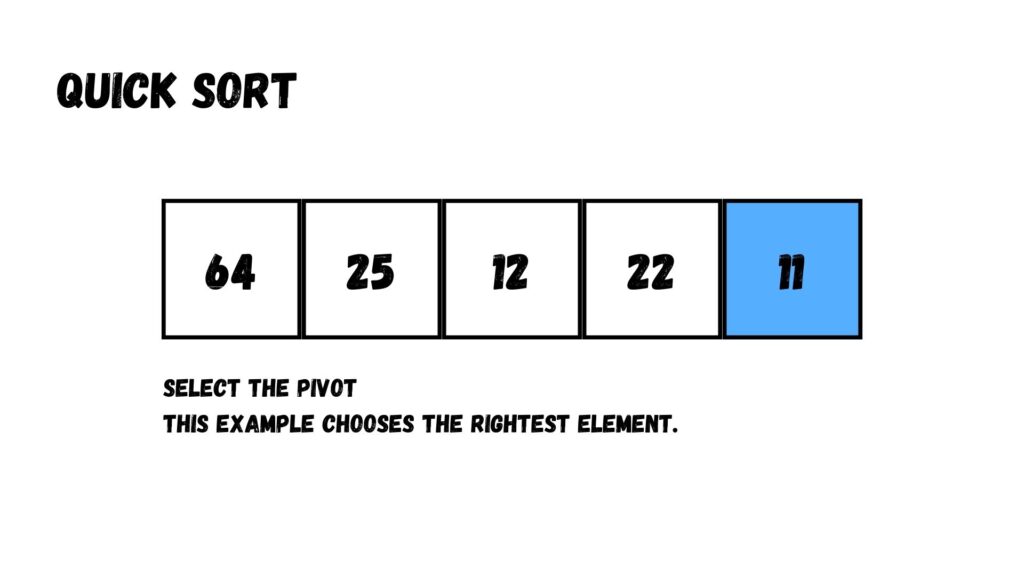
จากนั้นวนลูปใน Array เพื่อเช็คว่ามีค่าไหนที่มีค่าน้อยกว่าค่า Pivot จนถึงตำแหน่งสุดท้ายก่อนถึง Pivot ถ้ามีให้ย้ายข้อมูลไปตำแหน่ง i ของ Array
อย่างไรก็ดีค่า Pivot ที่เลือกนี้มีค่าน้อยที่สุดแล้ว ทำให้ไม่มีค่าไหนใน Array ที่ได้รับการย้ายข้อมูลไปทางซ้ายสุด พอวนลูปครบ เราย้ายค่า Pivot ไปยังตำแหน่งใน Array ที่ i + 1 (โดยค่า i เท่ากับ -1 แล้วเราจะได้ตำแหน่ง Array ที่ 0 ก็คือตำแหน่งด้านซ้ายสุด)

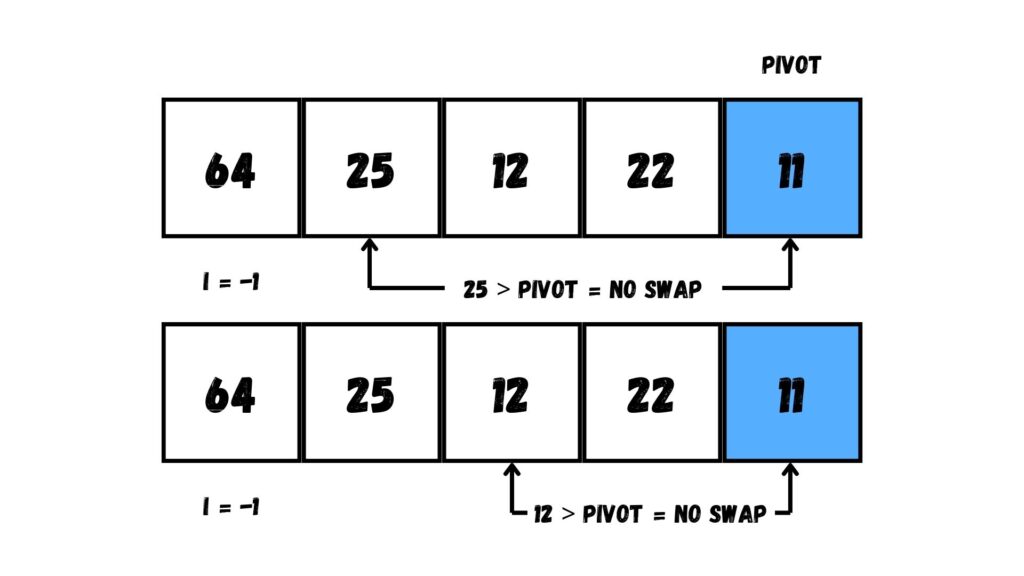
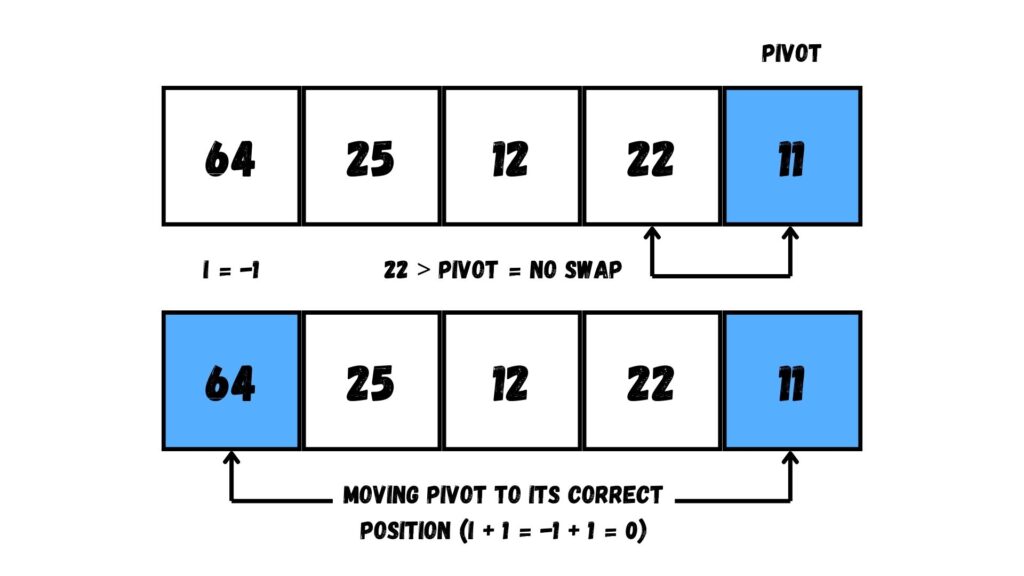
ต่อมา ให้เราแบ่งข้อมูลตาม Pivot โดยแบ่งเป็น
- ข้อมูลที่มีค่าน้อยกว่า
- กับข้อมูลที่มีค่ามากกว่า Pivot
โดยในตอนนี้ค่า 11 เป็นค่าที่น้อยที่สุดใน Array ทำให้ไม่มี Array ที่มีค่าน้อยกว่า มีแต่ Array ที่มีค่าที่มากกว่าเท่านั้น
ให้เราเลือก Array หลัง จากนั้นให้เราเลือก Pivot ที่ตำแหน่งสุดท้ายของ Array อีกเช่นเคย ร่วมกับกำหนดตำแหน่ง i ให้เท่ากับ 0 (ก็คือตำแหน่งถัดจากตำแหน่งซ้ายสุดของ Array ที่เราแบ่งออกมา)
ต่อมา วนลูปใน Array เพื่อนำค่าที่วนลูปมาเทียบกับ Pivot ถ้ามีค่าน้อยกว่าค่า Pivot ให้เพิ่มค่า i ทีละ 1 แล้วนำค่าใน Array นั้นสลับกับ Array ที่ตำแหน่ง i
วนลูปทำแบบเดิมไปเรื่อย ๆ จนกว่าจะถึงตำแหน่งสุดท้ายก่อนถึง Pivot
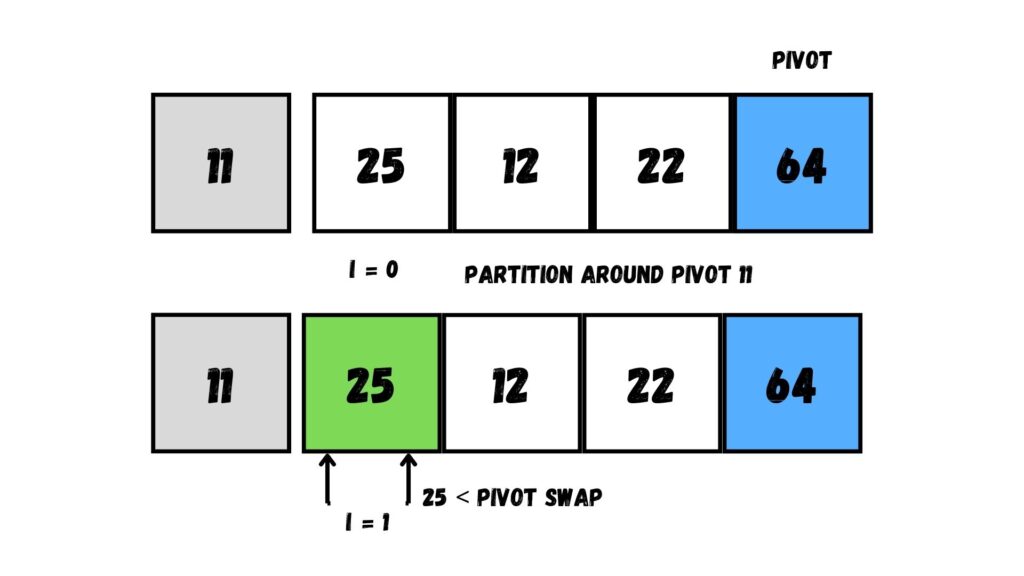

เมื่อถึงตำแหน่งสุดท้ายในการวนลูปแล้ว ให้เราย้ายค่า Pivot ไปยังตำแหน่งใน Array ที่ i + 1 ซึ่งมีค่าเท่ากับ 4 นั่นก็คือตำแหน่งเดิมของค่า Pivot นั้น
ถัดจากนั้น เราแบ่งข้อมูลตามค่า Pivot อีกเช่นเคย แต่ข้อมูลที่มีค่า 64 นี้เป็นข้อมูลที่มีค่ามากที่สุด ทำให้ไม่มี Array ที่มีค่ามากกว่า แต่มี Array ที่มีค่าน้อยกว่าเพียงอย่างเดียว
ให้เราเลือก Array ที่มีค่าที่น้อยกว่า จากนั้นเลือกข้อมูลอันสุดท้ายของ Array ที่แบ่งออกมา (= 22) เป็น Pivot และกำหนดตำแหน่ง i ให้เท่ากับ 0
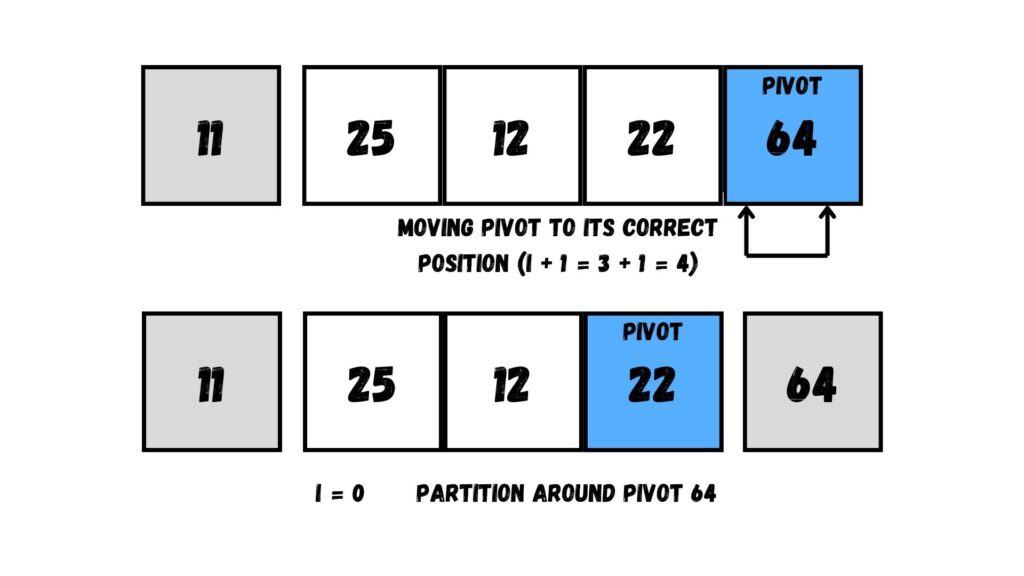
เมื่อเลือกค่า Pivot และกำหนดตำแหน่ง i แล้ว ให้เราวนลูปใน Array ที่แบ่งออกมา
เมื่อพบค่าที่น้อยกว่าค่า Pivot (ตัวอย่างเช่น 12) แล้ว ให้ขยับ i จาก 0 เป็น 1 แล้วสลับค่าระหว่างค่าที่น้อยที่สุดกับค่าที่ตำแหน่ง i เท่ากับ 1 (= 25)
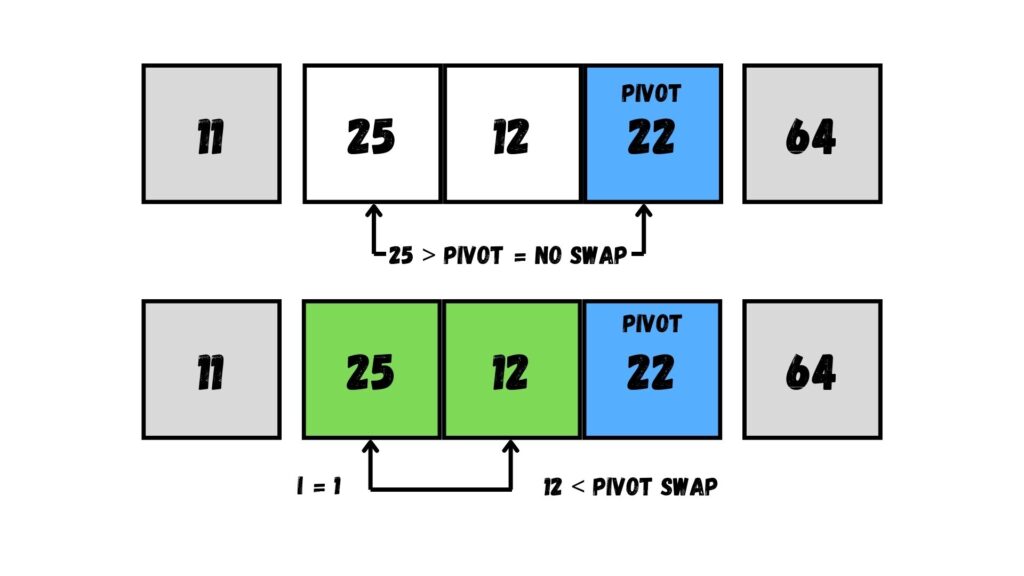
เมื่อวนลูปครบแล้ว ให้เราสลับค่า Pivot (= 22) กับค่าใน Array ตำแหน่งที่ i + 1 หรือเท่ากับ 1 + 1 = 2 (= 25)
เราแบ่งข้อมูลตามค่า Pivot อีกรอบ โดยเราจะได้ Array ทั้งหมด 2 Array ได้แก่ Array ที่มีค่ามากกว่า Pivot และน้อยกว่า Pivot ในแต่ละ Array มีข้อมูลทั้งหมด 1 ข้อมูล ซึ่งเราจะหาค่า Pivot และเรียงข้อมูลไม่ได้ ทำให้การเรียงอันดับข้อมูลด้วย Quick Sort ก็เสร็จเรียบร้อย

ผลลัพธ์ของการเรียงข้อมูลแสดงตามด้านล่างนี้
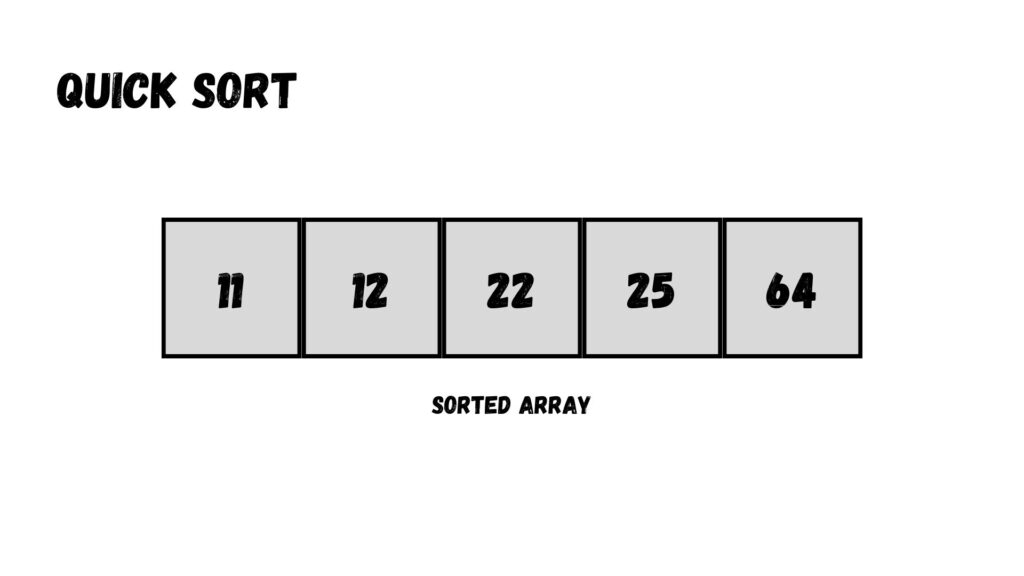
เราสามารถเขียนโค้ดได้ตามด้านล่างนี้
def quicksort(arr, low, high):
if high - low >= 2:
# After that, we make a quick sort.
mid_idx = partition(arr, low, high)
quicksort(arr, low, mid_idx - 1)
quicksort(arr, mid_idx + 1, high)
return arr
def partition(arr, low, high):
pivot = arr[high]
i = low - 1
for j in range(low, high):
if arr[j] <= pivot:
i += 1
arr[i], arr[j] = arr[j], arr[i]
# Save pivot and the last movable index
arr[i + 1], arr[high] = arr[high], arr[i + 1]
return i + 1Algorithm นี้มีประสิทธิภาพการทำงานตามระยะเวลาการทำงาน (Time Complexity) ในกรณีที่เป็น Average Case มีค่าเท่ากับ O(n log n) แต่กรณีที่เป็น Worst Case* มีค่าเท่ากับ O(n^2)
*Worst Case จะเกิดขึ้นในกรณีที่แบ่งข้อมูลใน Array แล้วได้ข้อมูลที่ไม่ Balanced กัน (Unbalanced Partitions)
และมี Auxiliary Space เท่ากับ O(1) ในกรณีที่ไม่ทำ Recursion แต่ถ้าทำจะมีค่าเท่ากับ O(n)
Algorithm นี้มีข้อดีได้แก่
- เป็นเทคนิคแบบ Divide and Conquer ทำให้ง่ายต่อการแก้ปัญหา
- เหมาะสมต่อการเรียงข้อมูลใน Dataset ที่มีขนาดใหญ่
- ใช้หน่วยความจำน้อย และมี Overhead ที่ต่ำ
อย่างไรก็ดี เทคนิคนี้มีข้อด้อย ได้แก่
- กรณีที่เกิด Worst Case เทคนิคนี้ให้ Time Complexity ที่มีค่าเท่ากับ O(N^2) กรณีที่เลือก Pivot ได้ไม่ดี
- ไม่เหมาะกับข้อมูลที่มีขนาดเล็ก
สรุป
Algorithms เป็นวิธีการแก้ไขปัญหาเป็นขั้นตอน 1 2 3 4 เพื่อให้เราแก้ไขปัญหาได้อย่างมีประสิทธิภาพมากที่สุด โดยเราจำเป็นต้องเลือกวิธีการเก็บข้อมูลที่มีโครงสร้างข้อมูล (Data Structures) ที่เหมาะสม
สองสิ่งนี้ที่เรียกว่า Data Structures กับ Algorithms เกี่ยวกับงานทางด้าน Data Engineer (หรืองาน Data) โดยเขียนโค้ดทำ Data Pipeline และเขียนโค้ดจัดการกับ Data ได้อย่างมีประสิทธิภาพ แถมยังนำไปใช้งานในด้าน Distributed Computing ได้อีก
โดยในบทความนี้เรานำเสนอวิธีการวิเคราะห์ประสิทธิภาพ Algorithm (Asymptotic Analysis) ร่วมกับนำเสนอ Big-O Notation
และยังนำเสนอ Searching และ Sorting Algorithms ได้แก่ Linear Search, Binary Search, Fibonacci Search, Selection Sort, Bubble Sort, Insertion Sort, Heap Sort, Merge Sort และ Quick Sort ครับ
สำหรับผู้อ่านที่เห็นว่าบทความนี้ดี มีประโยชน์ ให้กดไลค์ หรือกดแชร์ไปยังแพลตฟอร์มโซเชียลต่าง ๆ นอกจากนี้ ผู้อ่านยังติดตามได้่ใน Linkedin หรือ X (หรือ Twitter) ได้ครับ
แก้ไข
*แก้ไข ข้อผิดพลาดของรูปภาพในขั้นตอนการทำ Binary Search
อ้างอิง
- Algorithm – Saladpuk.com
- Why Data Structures? | Codecademy
- เราเอา Data Structure ไปใช้กันในส่วนไหนบ้าง ? – BorntoDev เริ่มต้นเรียน เขียนโปรแกรม ขั้นเทพ !
- Must-do DSA topics for Data Engineers | by Vishal Barvaliya | Towards Data Engineering | Medium
- Big-O Notation, Omega Notation and Big-O Notation (Asymptotic Analysis) (programiz.com)
- Asymptotic notation (thatthapalgorithmanalysis.blogspot.com)
- Analysis of Algorithms | Big-O analysis – GeeksforGeeks
- เข้าใจ Big O Notation แบบไฟลุกตีนไหม้ · rayriffy
- What is Big O Notation Explained: Space and Time Complexity (freecodecamp.org)
- Linear Search – Data Structure and Algorithm Tutorials – Geeks for Geeks
- Binary Search – Data Structure and Algorithm Tutorials – Geeks for Geeks
- Binary Search (With Code) (programiz.com)
- Fibonacci Search – Data Structure and Algorithm Tutorials – Geeks for Geeks
- Sorting Algorithms Explained with Examples in JavaScript, Python, Java, and C++ (freecodecamp.org)
- Selection Sort – Data Structure and Algorithm Tutorials – Geeks for Geeks
- Bubble Sort – Data Structure and Algorithm Tutorials – Geeks for Geeks
- Insertion Sort – Data Structure and Algorithm Tutorials – Geeks for Geeks
- Heap Sort – Data Structure and Algorithm Tutorials – Geeks for Geeks
- Binary Heap คืออะไร. สวัสดีครับวันนี้เราจะมาพูดกันถึง binary… | by Net vachirachat sawadditwat | Medium
- Merge Sort – Data Structure and Algorithm Tutorials – Geeks for Geeks
- Merge sort algorithm overview (article) | Khan Academy
- Quick Sort – Data Structure and Algorithm Tutorials – Geeks for Geeks
- Quicksort algorithm overview | Quick sort (article) | Khan Academy
- Time and Space Complexity Analysis of Quick Sort – Data Structure and Algorithm tutorials – Geeks for Geeks
© 2025. Nick Untitled. / Privacy Policy